I’m in the beautiful city of Avignon for the 3rd ISNPS conference, which is held in the extroardinary Palace of the Popes Convention center. I’ve been invited by Ricardo Cao to give a talk wednesday morning during on sampling methods for big graphs.
[Sports] UEFA Euro 2016 predictions – Comments
Last week we published the results of our prediction model for UEFA Euro 2016. Here are a few comments.
This Euro is undecided
Our model gives fairly close probabilities of winning. To us, this suggests that the competition is fairly open and that no team is a clear favorite before the competition starts (we really hope to see that change after a few matches!)
One could object that this merely shows that our model is unable to predict an outcome with adequate confidence, so we ran the simulations after injecting an artificially low variance in our model, and results for the top teams turned out to be very similar: no clear favorite emerged.
Historically, the European Championship has always been somewhat undecided. Whereas only 8 different teams ever became World Champions (20 editions of the World Cup were held), 9 different teams have already won a European Championship in just 14 editions! In some cases, complete underdogs eventually won the title (for example Denmark in 1992 or Greece in 2004).
France is one of the favorites
The home team is every other’s model favorite! Check out Goldman Sachs’ or a model built by Austrian researchers based on bookmakers’ odds. Clearly, the home advantage is key here, although recently France has proven able to score quite a number of goals, which is an important feature of our model. The model’s favorite is Belgium (who are, the start of the competition, 2nd in the Fifa rankings), but Germany, Spain and England are very close.
Interestingly, even if our model selects France as one of its favorite, it predicts that the group phase won’t be as easy as it seems. For example, the most likely scenario for the opening match is a draw. The probability of reaching the second round is high (86%), but it’s only the fifth highest of values (which might be surprising if you consider that France’s first round opponents are really far behind in the Fifa/Elo rankings). This is very different from other models and bookies, who make France a very heavy favorite to end up at the first place of the group.
As a supporter of France, this reminds us a few (good) memories. In 2000, France only finished second of its group to the Netherlands (and still won the competition), while in the 2006 World Cup, France barely qualified among relatively weak teams, and still managed to reach the final.
Zlatan may not be enough
Altough Sweden, partly thanks to its legendary striker Zlatan Ibrahimovic, is generally said to be a fairly good team, it has the lowest probability of reaching the round of 16 (24.1%), slightly behind Iceland and Albania. In fact, Sweden was very unlucky during the draw and ended up in the so-called “group of death” along with two top tier teams (Belgium and Italy), and an outsider (Ireland) that our model predicts not so bad.
Are Switzerland and Hungary undervalued?
The biggest difference between our model and the bookies’ odds (or the other models) is the relatively high probability we put on Switzerland’s win (6% for us, 1% for Goldman Sachs for instance). It’s hard to really say why our model predicts they’ll fare so well, but we’re definitely impatient to see if this checks out 🙂
Our model also says Hungary is generally under-estimated: to it, the heirs of the “Magikus Magyarok” might very well fight for second place in Group F, while in most predictions they finish dead last.
EDIT: a previous version of this article presented France as the model’s favorite, which was the consequence of a bug that occurred for the second-round probabilities. It is now corrected. Other conclusions are unchanged.
[Sports] UEFA Euro 2016 Predictions – Model
Today we’re launching our own predictions for UEFA Euro 2016 that starts next week.
A model for football: state of the art
There are many ways to build a model to predict football results. The Elo ranking system is commonly used. As it name indicates, it relies on a ranking of the international football teams, either the official FIFA ratings (which are widely known as poorly predictive of a team’s strength) or a custom made Elo ranking. A few Elo rankings are available on the Internet, so one possibility was to use one of these to compute probabilities for each game (via a very simple analytical formula). But we wanted to do something different.
When FiveThirtyEight created a nice viz of their own showing odds for the men’s and women’s world cups, their model was based on ESPN’s Soccer Power Index (SPI). The principle of the SPI is quite simple: compute expected scored and against goals for each team under the assumption it plays against an “average” football squad. Then run a logistic regression to predict the outcome of any two teams, based on their expected performance against the “average” team. SPI takes an impressive amount of relevant parameters into account (including player performance), and has generally proven itself reliable (although FiveThirtyEight’s predictions always seemed a tad overconfident to me!).
Our very own model
For our model, we liked the principle of the SPI very much, but we wanted to try our own little variation. So we kept the core feature of the SPI: computing the expected goals scored and against for each team, but we chose to directly plug these results into our simulations (i.e without the logistic regression). Of course, due to lack of time and resources, our model will be way less sophisticated than ESPN’s (there was no way we could include player performance for example), but still the results might be worth analyzing!
So, for each one of the 24 teams competing, we’re trying to predict the quantitative variable that is the number of goals scored (and against) for each game. Of course, we’re going to use all our knowledge of machine learning to achieve this 😉 Our training data is composed of the 1795 international games played by the 24 teams that qualified for UEFA Euro 2016 between 2008 and 2016 (excluding the Olympics, which are too peculiar in football to be relevant).
We dispose of 1795 observations, for each of which we know: the location of the game, the teams that played, the final score and the type of the game (friendly, world cup qualifier, etc.). We matched each team to its Fifa ranking at the closest date available, and determine which team had home court advantage (if any).
Then we ran the simplest of regression models: a linear regression on year, team (as a categorical variable), dummy variable indicating if team plays at home or away, type of match and FIFA rankings of both teams. Before even thinking of using this model for simulations, we have to look at how it performs. And a lot of think indicates that it is too unsophisticated. The most telling example might be the prediction of large number of goals. Let’s plot the number of goals scored vs. the FIFA ranking of the opposing team.
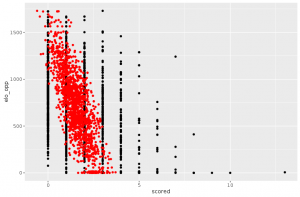
You can see on the right side of the plot that it’s not that rare that a large number of goals is scored, especially when playing a very weak team. However, the linear model is unable to predict more than 4 goals scored in a game. This can be a huge problem for simulations as ties are broken by number of goals scored at Euro.
The idea is thus to combine several linear models to get a more sensible prediction. This can be done using regression splines, for which the parameters are chosen using cross-validation.
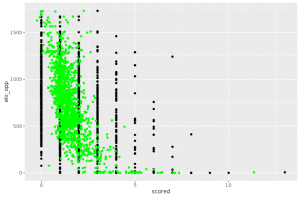
On number of ways, this model is much more satisfying than the first one. Regarding the large values of number of goals scored, the above plots show that our model is now able to predict them 🙂
Simulations and results
Our model gives us expected values for number of goals scored and against, as well as a model variance. We then simulate the number of goals with normal error around the expected value. We do this 10000 times for each match and finally get Monte-Carlo probabilities for the outcome of each group phase match, as well as odds for each team to end at each place in its group and to qualify to each round of the knockout phase.
The results can be found here, and I will post another article later to comment them (which really is the fun part after all!).
[Sampling] Coucher pour réussir ?
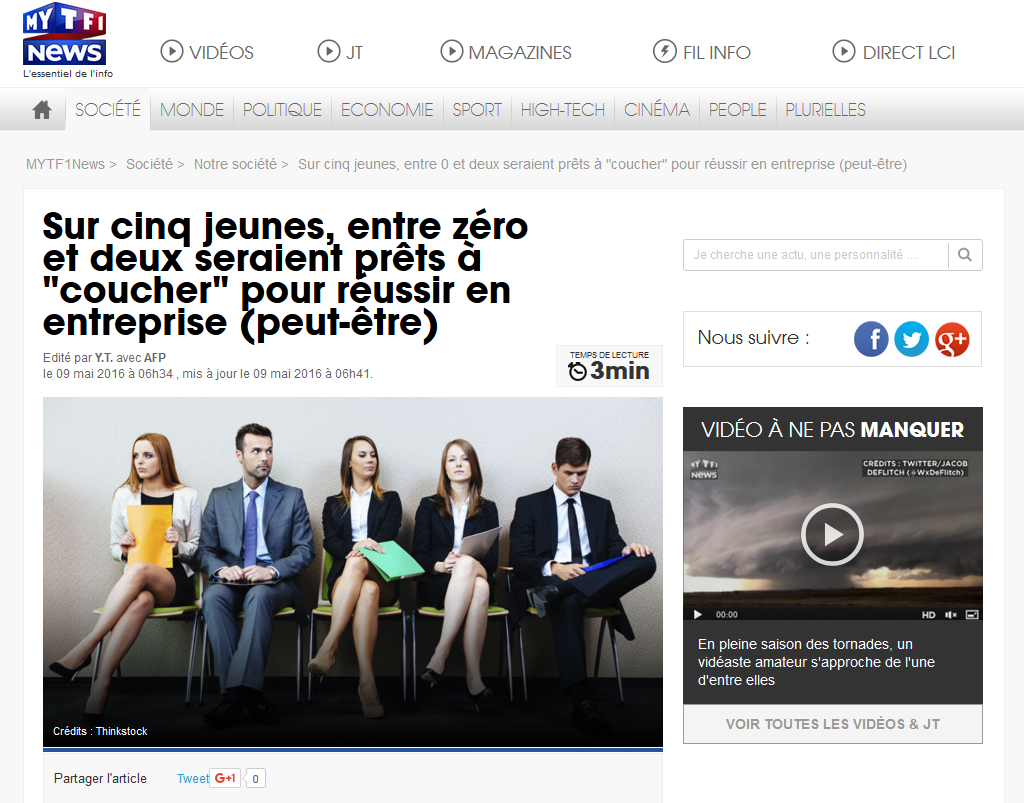
Je commence ma semaine en tombant sur un article de LCI qui indique qu’une enquête OpinionWay estime qu’un jeune sur cinq serait prêt à “coucher” pour réussir en entreprise (note : l’info a été en fait reprise dans beaucoup de quotidiens ce lundi matin). On note au passage la magnifique illustration qui montre cinq jeunes salariés … je suppose qu’il faut se demander lequel parmi les cinq est sur le point de coucher pour réussir ?
Essayons d’avoir un regard critique sur ce chiffre annoncé. Souvenons-nous que lorsque l’on fait un sondage, on choisit de n’interroger qu’un petit nombre d’individus, à qui on pose les questions qui nous intéressent. Bien entendu, ce serait trop coûteux d’interroger 66 millions de français au sujet de leur intention de coucher pour réussir (c’est l’intérêt du sondage), mais on paye tout de même un prix : la statistique obtenue aura une certaine imprécision, aussi appelée erreur d’échantillonnage. Essayons d’estimer cette “imprécision”.
Les informations données sur le sondage effectué montrent que l’échantillon a été construit “de façon représentative” (si vous voulez savoir ce que je pense de ce terme, vous pouvez lire cet article) par la méthode des quotas. Cela signifie que les proportions de jeunes salariés de 18-24 ans dans la population et dans l’échantillon sont censées être égales. D’après des statistiques diffusées par Pôle emploi, les 18-24 ans représentent environ 9% du nombre de salariés total. Les 18% de jeunes salariés prêts à coucher pour réussir sont donc dans l’échantillon au nombre de :
0.09 \cdot 1060 \approx 95.4
\end{align*}
Cette “statistique” ne repose donc que sur les réponses de 95 personnes, et non pas la totalité de l’échantillon (notez qu’il est probable que je surestime le nombre de jeunes salariés de l’échantillon car celui-ci semble construit sur le total de la population et non sur le total de salariés). On peut utiliser cette valeur pour calculer un intervalle de confiance pour la statistique, donné par la formule :
\hat{IC} &= \left[ 0.18 \pm 2\cdot \sqrt{\dfrac{0.18 \cdot (1-0.18)}{95}} \right] \\
&\approx [0.10 ; 0.26]
\end{align*}
Comme prévu, l’intervalle de confiance est très large : la valeur estimée à 18% est comprise entre 10% et 26% au seuil de confiance de 95%, soit entre “un jeune sur dix” et “un jeune sur quatre”. Et il s’agit uniquement de l’erreur d’échantillonnage ! Les sondages en général sont sujets à beaucoup d’autres sources d’erreurs (voir par exemple le dernier chapitre de ce cours pour plus de précisions). Par exemple, pour cette enquête, le questionnaire était rempli par les individus échantillonnés sur une page web. Le questionnaire n’est pas diffusé ici, mais imaginez que cette question soit la 198ème d’une série de 200, pourrait-on accorder une grande importance aux réponses données par ces 17 individus à cette question ? La formulation de la question peut également influer sur la réponse données par les individus interrogés.
Prenant tout cela en compte, on peut réécrire la version “statistiquement honnête” de l’article de LCI :
Finalement c’est peut-être mieux que je ne sois pas journaliste 😉
[Dataviz] Odonymie et couleur politique
Les noms de rue peuvent être parfois un sujet politique sensible, comme l’a montré une actualité récente. L’odonymie (ou étude des noms des voies de communication) a déjà donné lieu à quelques dataviz sympathiques, comme par exemple sur le blog datamix, le site PatronyMap ou sur Slate. Disposant d’une base de données de noms de rues en France Métropolitaine, nous avons cherché à notre tour à illustrer le lien entre odonymes et politique par une petite dataviz.
On dispose de la liste des noms de rues pour 1470 grandes villes, que l’on classe en deux catégories “Droite” et “Gauche” suivant la couleur politique de leur mairie en 2012 (738 communes à gauche et 732 à droite). On entraîne ensuite un modèle de classification naïve bayésienne sur le TF-IDF constitué par cette liste d’odonymes, que l’on optimise classiquement par validation croisée sur sa qualité prédictive. Etant donnée une liste de noms de voies, le classificateur choisi permet d’identifier correctement la couleur politique de la ville dans environ 70% des cas. Ce chiffre plus élevé que ce à quoi nous nous attendions montre que l’influence de la politique sur les noms de rues (ou tout du moins la corrélation entre les deux) est réelle. Enfin, prédire correctement la couleur politique d’une ville à partir d’un ou ou plusieurs noms de rues n’est que peu intéressant en soi : le modèle entraîné vaut surtout pour son pouvoir explicatif (modèle de régression). C’est pourquoi on utilise les probabilités calculées par le classificateur pour construire une “typicité d’un nom de ville de droite/gauche”, qui est indiquée par la jauge dans notre dataviz.
En faisant tourner le modèle sur notre base de données, les valeurs des probabilités (typicités) obtenues vont de 0.25 à 0.75 (en prenant la convention “0 = gauche” et “1 = droite”), avec plus de 99% des valeurs entre 0.3 et 0.7. Notre jauge est recalibrée en conséquence avec un minimum à 0.3 et un maximum à 0.7, de manière à pouvoir observer correctement les valeurs.
En faisant quelques tests, on s’aperçoit d’une typicité bien plus marquée à gauche qu’à droite (le recall de notre modèle est d’ailleurs supérieur à 90% pour les villes de gauche). A première vue, les odonymes les plus typiques de la droite semblent très “traditionnels” (par exemple Rue de l’industrie ou Rue des Fleurs) alors que les odonymes les plus typiques de la gauche mettent plutôt en avant des personnalités (rue Jean Jaurès, rue Salvador Allende, etc.). Partant de ce constat, on aurait très envie de pouvoir tester si le fait de renommer une rue est plus le fait de la gauche que de la droite, mais on ne dispose pas de données sur les renommages qui permettraient de le faire. Peut-être une prochaine fois ?
Certaines disparités régionales transparaissent également (testez par exemple rue des Alpes vs. rue des Pyrénées ou rue Eric Tabarly vs. rue des Cigognes), et curieusement le type de voie est parfois très influent (“quai” penche à gauche alors que “traverse” penche à droite). Les noms issus du communisme quant à eux penchent certes à gauche, mais peut-être pas autant que l’on aurait pu imaginer (avenue de l’Union Soviétique, avenue Karl Marx). Il faut se souvenir que notre modèle prend en compte la couleur politique de 2016, et que l’orientation politique de certaines villes ont pu changer depuis le moment où ces rues ont été baptisées. Enfin, gardez à l’esprit que cette dataviz n’est que l’illustration d’un modèle et qu’a fortiori rien de ce qui peut être indiqué n’a de valeur sociologique ou politique. N’hésitez pas à mener vos propres tests, et à nous envoyer/tweeter vos trouvailles les plus intéressantes !
[Sports] Don’t miss a shot in biathlon races
Today, I want to speak about my favorite sport to watch on TV, which is biathlon (the one which involves skiing and shooting at things. Who doesn’t love that?). I really enjoy to follow the races, and not only because the best athlete at this moment is a french one (go Martin!), but because the shooting part seems so crucial and stressful. This leads me to wonder about how much missing a shot is relevant for the ranking in the end of the race. Let’s find out!

Gathering some data
My idea is to do some basic analysis on data about the results of many biathlon races, in order to evaluate if there is some form of correlation between the final ranking and the number of shot missed. This requires to first gather the data. The results are stored on multiple sites: obviously Wikipedia pages of the championships, but this website is much more detailed. I’m going to use some of the results between 2007 and 2015. I won’t use all of the races because I want to have comparable results: I’m going to only consider the races where the number of competitors is between 50 and 60. This allows me to interpret the results about final ranking with a similar scaling system for all the races. Moreover, the specificity of biathlon is that the rules are very different from a format to another (see this Wikipedia article for more informations), and I can’t easily discriminate my data between them. Using a limitation on the number of participants is a way to limit the width of the spectrum of formats considered. Well, let’s forget these technicalities and analyse the data!
Don’t miss a shot!
So, the idea is to put in regard the number of shots missed and the final ranking. Fun fact: the number of shot during a race is 20, but the maximum number of shot missed during a race I analysed is only 9. That’s not really a surprise if you frequently watch biathlon, because missing that much shots usually means that you’re going to finish in last place. I’m going to use a heat map in order to show the correlation. An heat map is a form of 2D data vizualisation which is based on a spectrum of colors. Thedarker the color is, the more important the value is. The idea here is to put in rows the final ranking, and in columns the number of shots missed. Here is what we obtain:
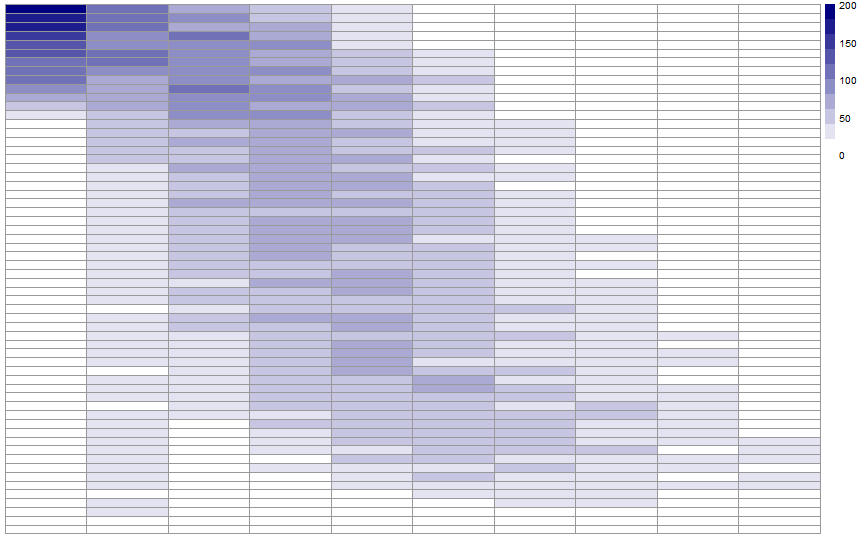
There results directly show that:
- There is a clear diagonal on the heat map. This isn’t really surprising: that means that everytime an athlete misses a shot, his final ranking goes lower. This is our first result: missing shot are penalties. What a surprise!
- There is also a very dark blue area in the first column, at the top of the diagram. This means that most of the time, doing a clear round leads to a very good ranking in the end.
- But it is clearly possible to win a race while missing some shots! The first row is filled with dark blue in the first few columns.
Don’t miss a prone shot!
As you may know, there is two different types of shooting during a biathlon race: the prone shot, where the athletes are lying on the floor; this position helps them to stabilise their aim. The other type is the standing shot, which is much more difficult. Therefore, it might be interesting to deal with the two phases of shooting separately. Let’s start with the prone shot, as this is usually the first phase of shooting during a race.

We see the same pattern as the total of shots. The top of the first column is much darker than before: this is because of two things. First, it is usual that a lot of athletes don’t miss a shot during the prone shot phase. And that means that missing a prone shot is much more a sign of a bad shooting, which leads to a bad ranking at the end. This point is very important: we’re not evaluating results in a vacuum: and missing a shot usually means that the athlete is in a bad shape compared to the others, and therefore has a bad ranking. But this also means that missing a shot during the first phase raise the odds of missing shots during the other phases.
Let’s have a look at the heat map for the standing shots.
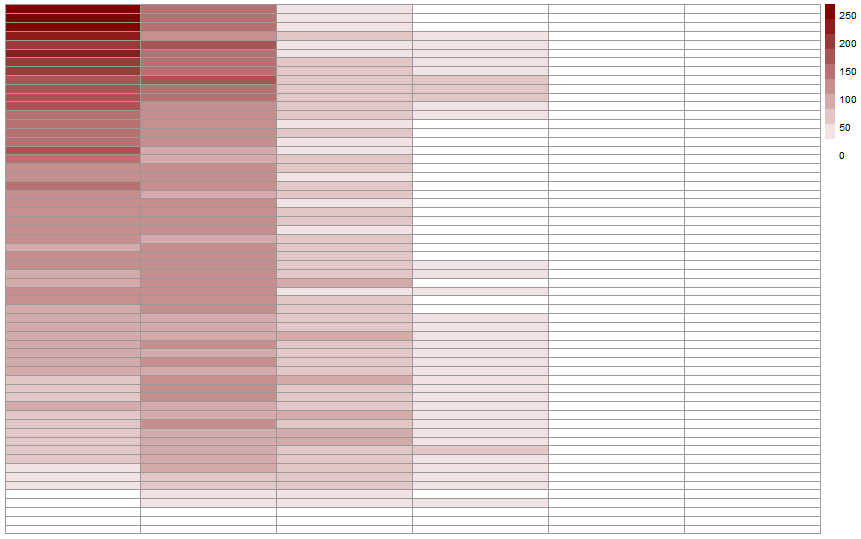
As expected (because the initial one is the combinaison of these two heatmap), we’ve a much more dispersed heat map. Missing a standing shot is something that happens to pretty much everyone, even the best athletes.
Is the starting order relevant?
I add to the analysis a last factor: the starting order, which is linked to the expectation of results of the athlete (based on a global ranking, or on the results of another race). The heat map showing the correspondances bewteen the final ranking (still in rows) and the starting order (in columns) shows a clear diagonal line: the expectation seems relevant.

In order to do a much more indepth analysis, I’m going to perform a linear regression on these variables. I want to know if the final ranking is explained by the initial order, the number of prone shots missed and the number of standing shots missed. This linear regression will also help me to evaluate how big of an impact these three variables have on the final outcome. Let’s have a look at the results:
Call:
lm(formula = ranking ~ prone shots + standing shots + starting order)
Residuals:
Min 1Q Median 3Q Max
-60.625 -8.483 -0.101 9.268 45.295
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.816571 0.212517 27.37
The three variables of the model are statistically significant, which means that they do have a relation with the final ranking. Understanding the coefficient for the Starting Order is kind of tough, but the two other coefficients are much more easier to analyse:
- When you miss a prone shot, you lose about 5 places at the end of the race
- When you miss a standing shot, you lose about 1 place at the end of the race
Obviously, these results are only valid on average. But this is kind of a fun way to comment biathlon shootings! “Oh, you just lost 10 places!”.
[Sampling] Combien de salons de coiffure ont un jeu de mots dans leur nom ? (Deuxième partie)
Suite de notre première partie. Nous avions utilisé une méthode de sondage pour déterminer le nombre de salons de coiffure dont le nom est un jeu de mots. Dans cette seconde partie, nous allons essayer d’utiliser une méthode d’apprentissage pour estimer ce nombre. L’idée sera d’entraîner un modèle à reconnaître si une enseigne de coiffure présente un jeu de mots ou non. C’est parti !
Jeu d’entraînement
Il faut commencer par constituer un “jeu d’entraînement” (ou training set), qui comportera des noms avec et sans jeu de mots, de manière à ce que le modèle choisi puisse construire une règle de classification. Ce jeu d’entraînement, nous allons devoir le constituer à la main. Comme je n’ai pas envie de passer mon dimanche entier à classer des noms de salons de coiffure suivant qu’ils contiennent un jeu de mots ou non (je serais obligé de mentir si on me demandait ce que j’ai fait de mon week-end à la machine à café lundi matin) je choisis de me limiter à 200 enseignes, que je vais tirer aléatoirement dans la base.
Petite remarque supplémentaire : si je tirais ces noms avec une probabilité uniforme (comme on l’a d’abord fait en première partie), ma base comporterait environ 10 enseignes avec jeu de mots contre 190 enseignes sans (puisque, d’après la première partie, le taux de salons de coiffure avec un jeu de mot vaut environ 5%). Avec simplement 10 noms comportement un jeu de mot dans notre base de références, faire classer efficacement les noms de salons par un modèle ne serait pas chose aisée… Je choisis donc d’utiliser à nouveau un tirage stratifié (comme en première partie), de manière à équilibrer les données sur lesquelles le modèle va être entraîné.
Avant de passer à la suite, je réserve 50 noms parmi mes données d’entraînement que j’utiliserai uniquement pour tester la qualité de mon modèle. Le modèle sera donc entraîné sur 150 noms de salons, parmi lesquels environ 50% présentent un jeu de mot (je nomme ces données “jeu de développement”).
Une nécessaire sous-estimation
Il va s’agir de choisir un classificateur d’apprentissage qui présente de bonnes performances sur des données issues de Natural Language Processing (NLP). Le but est que notre modèle soit capable de reconnaître un jeu de mots similaire à ceux qui sont contenus dans le jeu de développement. Des noms similaires à une enseigne contenue dans le jeu de test devraient être correctement classés si les différences sont mineures (quelques lettres, l’ordre, une préposition en plus ou en moins, etc.). Par exemple, si le jeu de développement contient “FAUT TIFF HAIR”, il est bien possible que “FAUTIF HAIR” ou “FAUT TIF HAIRS” soient correctement classés. A fortiori, tous les noms strictement identiques à ceux du jeu de développement seront correctement classés. Par contre, on ne peut pas raisonnablement s’attendre à ce que le modèle soit capable de reconnaître un jeu de mots très différent de ceux qui seront contenus dans cette base de données.
Finalement, il faut s’attendre à ce que cette façon de procéder aboutisse à une sous-estimation du nombre de salons de coiffure avec jeu de mots. Pour le vérifier, on pourra comparer avec l’intervalle de confiance établi en première partie.
Le choix du modèle
J’utilise l’excellent librairie python scikit-learn, que j’utilise pour tester différents types de classificateurs. Bien souvent en machine learning, il s’agit de tester rigoureusement différents modèles et différents choix de paramètres comparativement les uns aux autres. Dans notre cas, je cherche simplement un classificateur suffisamment performant pour aboutir à une conclusion à peu près robuste. Je me contente donc de quelques essais à la main pour effectuer mon choix de modèle. J’effectue ensuite un petit grid search pour tester différents choix de paramètres. Dans le cas du choix de modèle comme du grid search, j’utilise une validation croisée pour choisir le meilleur modèle. Mon classificateur final est donc :
vectorizer = TfidfVectorizer(ngram_range=(1, 3), analyzer='char',
use_idf=False, stop_words=["SARL", "SAS", "SA"])
clf = Pipeline([
('vec', vectorizer),
('clf', SGDClassifier(loss="hinge", penalty="l2")),
])
clf.fit(docs_train, y_train)
Je peux enfin tester la performance de mon modèle sur le jeu de test de 50 noms que j’ai mis de côté :
| Classé “avec jeu de mots” | Classé “sans jeu de mots” | |
| Sans jeu de mots | 17 | 7 |
| Avec jeu de mots | 11 | 15 |
Par ailleurs, le jeu de test contenait 26 noms avec jeu de mots. L’estimation issue du modèle donne 22 noms avec jeu de mots, ce qui est cohérent avec le fait qu’on s’attend à obtenir une sous-estimation.
Petits tests à la main
Avant de faire tourner le classificateur sur l’ensemble de la base, j’effectue quelques petits tests à la main, avec des noms d’enseigne inventés. Comme prévu “CREA TIFFS”, “FAUT TIFF HAIR” et “FAUX TIFF HAIR”, proches de certains noms du jeu de développement, sont bien reconnus comme présentant un jeu de mot . “HAIR DRESSER” et “COIFFURE JEAN MICHEL” sont également correctement classés, en tant que noms ne présentant pas de jeu de mots. Je teste ensuite “LA CHAMBRE A HAIR”, “VOLT HAIR” et “LE SAVOIR F HAIR” (merci au tumblr lolcoiffeurs pour les idées !), sans grand espoir car ces jeux de mots me semblent trop éloignés de ceux présents dans le jeu d’entraînement. Et pourtant, les trois sont bel et bien reconnus comme jeux de mots ! Mon dernier test, “DE MECHE AVEC VOUS”, n’est lui pas correctement reconnu. Cela ne m’étonne pas outre mesure, car le nom de salon qui s’en approchait le plus dans mon jeu d’entraînement était “MECH EN LOOK”, qui ne contenait même pas le mot “MECHE” en entier. Finalement, je suis plutôt agréablement surpris des performances du modèle (comme souvent en learning , même si dans notre cas, le modèle et son ambition sont très modestes).
Les résultats
En exécutant notre classificateur sur toute la base des noms de salons, on obtient une valeur d’estimation de :
916, soit 3% de coiffeurs (contre environ 5% par la méthode par sondage)
présentant un jeu de mots dans leur enseigne. Ce chiffre correspond à l’estimation basse obtenue par sondage en partie 1. Ceci est cohérent avec notre remarque faite plus haut : ce chiffre obtenu par apprentissage est une sous-estimation du nombre total.
Dernière remarque : ce modèle est valable uniquement pour les enseignes de salons de coiffure. On pourrait appliquer une méthode similaire pour déterminer le nombre de jeu de mots parmi les enseignes d’un autre secteur (les boulangeries par exemple), en changeant le training set et en ajustant le modèle. Mais trouver une méthode générale pour reconnaître ce qui constitue ou non un jeu de mots en français serait une autre paire de manches !
Note 1 : L’image-titre est issue d’une note de Boulet, qui possède un blog bd très sympa que je vous encourage à aller voir !
Note 2 : en échangeant à propos de cet article, on m’a fait remarquer que notre définition du jeu de mot n’incluait pas par exemple le cas d’un jeu de mot “pour initié” sur le quartier dans lequel est situé la boutique ou sur le nom des entrepreneurs. Je précise donc que notre définition recouvre plus ou moins les jeux de mots “compréhensibles par tous” 😉
[Sports] Best/Worst NBA matchups ever
Earlier this month, the Philadelphia 76ers grabbed their first (and for now, only) win of the season by beating the Lakers. That night, checking for the menu on the NBA League Pass, I quickly elected not to watch this pretty unappealing matchup. Though I couldn’t help thinking that it is a shame for franchises that have both won NBA titles and see legends of the game wear their jerseys. During many seasons, a Lakers-Sixers game meant fun, excitement and most important of all excellent basketball. And I started wondering what were the best and worst matchups throughout NBA history.
Data and model
My criterion to evaluate these matchups will be the mean level of the two teams during each season. In fact, by “good” matchup I mean a game that feature two excellent ball clubs, making it an evening every NBA fan awaits impatiently as soon as the season calendar is made available. On the contrary, a “bad” matchup is a game whose only stake will be to determine draft pick orders. My criterion does not predict the actual interest of watching these games: a confrontation between two top teams might very well be pretty boring if the star players are having a bad night (or if the coach decides to bench them). Also, a contest between two mediocre teams might very well finally be a three-OT thriller with players showing excellent basketball skills. In fact, my criterion only holds from an historical perspective (or in the very unlikely case that you have to choose between the replay of several games without knowing when these games were played 🙂 ).
The level of each team is estimated using the excellent FiveThirtyEight NBA Elo rankings. Then, to rank the 435 possible matchups between the 30 NBA franchises, I will average the mean level of every two teams for all years between 1977 and 2015 (I chose to limit the analysis to after the NBA-ABA merger of 1976 so as to avoid dealing with defunct franchises). You can found the R codes I used on my GitHub page.
The best matchups
Of course, our method values regularity, so it’s no surprise we find at the top matchups between the teams that have been able to maintain a high level of competitivity throughout the years. In fact, the best matchup ever is “Lakers – Spurs”, two teams that have missed the playoffs only respectively 5 and 4 years since the 1976-1977 season! “Celtics – Lakers” comes in 6th: basketball fans won’t be suprised to find this legendary rivalry ranked up high. It might even have been higher if I had taken seasons prior to the merger into account. The first 10 matchups are:
1. “Lakers – Spurs”
2. “Lakers – Suns”
3. “Lakers – Trailblazers”
4. “Lakers – Thunder”
5. “Suns – Spurs”
6. “Celtics – Lakers”
7. “Spurs – Trailblazers”
8. “Spurs – Thunder”
9. “Rockets – Lakers”
10. “Spurs – Heat”
The worst matchups
The worst matchup ever is “Timberwolves vs. Hornets”. Thinking about the last few years, I have to admit that these games were clearly not among my favorites. Poor Michael Jordan’s Hornets trust the last 7 places on the ranking, thanks to the inglorious Bobcats run.
Among the most infamous matchups ever are:
425. “Clippers – Timberwolves”
426. “Clippers – Nets”
427. “Raptors – Hornets”
428. “Wizards – Timberwolves”
…
434. “Kings – Hornets”
435. “Timberwolves – Hornets”
I really hope the owners of these franchises are able to turn the tide and put their teams back up in the rankings soon!
[Sampling] Combien de salons de coiffure ont un jeu de mots dans leur nom ? (Première partie)
Nous connaissons tous une boulangerie, ou un salon de coiffure, qui a un jeu de mots dans son nom (“L’Hair du temps” ?), mais est-ce vraiment si répandu ? Essayons de répondre à cette question. Il y a plusieurs manières d’aborder ce problème : utiliser une approche de type apprentissage (mais il n’est jamais simple de faire comprendre l’humour à un ordinateur, et nous discuterons de cela plus tard), ou une approche de type sondage (ce qui sera fait dans un premier temps, dans cet article).
L’idée derrière cette approche consiste à se dire que juger la totalité des noms des salons de coiffure serait assez long (il y en a plusieurs dizaines de milliers) et que l’on va donc seulement s’intéresser à un petit échantillon (qui ne sera pas “représentatif” !) sur lequel on fera le travail de juger si le nom correspond à un jeu de mots ou pas.
Quelques considérations pratiques tout d’abord : nous avons un jeu de données composé de 30 083 entreprises françaises dont l’activité principale est dans le domaine du 9602A, ce qui dans le monde merveilleux des nomenclatures de la statistique publique, signifie que ce sont des entreprises dans le domaine de la coiffure, donc des salons de coiffure. On va également considérer qu’une taille raisonnable pour le travail de détection des jeux de mots est de prendre n = 200.
Première tentative
Nous allons donc extraire un échantillon de 200 SIREN de notre base, en utilisant un sondage aléatoire simple pour les choisir. Qu’entend-on par sondage aléatoire simple ? Comme son nom l’indique, il s’agit d’une technique basique de sondage qui repose sur deux postulats : on peut sélectionner tout le monde avec la même chance, et on veut aboutir à une taille fixe. Une représentation possible de ce type de sondage consiste à imaginer une urne avec les 30 083 boules qu’on mélange, puis on extrait une à une des boules jusqu’à en avoir le nombre souhaité, ici 200. Ce type de sondage est facile à mettre en pratique ; et il est facile d’utiliser les résultats obtenus pour avoir une estimation sur la population totale, et même une idée de la précision de cette estimation. On peut se référer au cours suivant pour une présentation plus détaillée.
Nous avons donc suivi ce plan de sondage, et nous avons un échantillon de 200 noms de salons de coiffure. Il reste maintenant à analyser les résultats pour détecter les jeux de mots : cette phase est forcément subjective, mais j’ai essayé ici de prendre la définition la plus large possible de jeu de mots, c’est à dire à chaque fois qu’il peut y avoir un double sens ou un jeu sur la prononciation de mots. Regardons plutôt quelques exemples trouvés dans l’échantillon :
Atmosp’hair, Posi’if, Aux mains d’argent, L’art de Pl’Hair, Diminu Tif, FauTif’Hair…
J’arrive au total à 13 jeux de mots, ce qui nous donne un pourcentage de jeux de mots de 6,5% parmi les salons de coiffure. L’utilisation d’un sondage aléatoire simple permet de garantir que cette estimation est sans biais (c’est un estimateur d’Horvitz-Thompson (en) du ratio), c’est à dire que, en moyennant sur tous les échantillons que l’on peut obtenir, on obtient la vraie proportion sur la population totale des salons de coiffure. Cela signifie en particulier que l’estimation que nous avons est fiable.
Cependant, cela ne signifie pas qu’elle est précise ! Prenons un exemple simple. On a deux individus A et B, avec une valeur de 0 pour A et de 100 pour B, et que l’on veut estimer la moyenne des valeurs dans la population, qui vaut 50. Lorsque l’on réalise un sondage aléatoire simple d’un individu parmi les deux, nous allons avoir la moitié du temps A et donc une estimation de 0, et la moitié du temps B et une estimation de 100. Cela donne bien 50 en moyenne : pourtant dans une réalité où l’on ne peut pas répéter le tirage des échantillons, on aurait juste l’observation de B (par exemple), et donc un estimateur de 100. Cette estimation est très imprécise : cela vient de la faible taille de l’échantillon (1 n’est pas suffisant), et de la très grande hétérogénéité de la population (si A avait une valeur de 1 et B de 2, on serait plus proche de la vérité). On peut aussi voir, en anglais, l’exemple des éléphants de Basu (en), bien connu des étudiants en théorie des Sondages.
Il existe une formule permettant de calculer la variance de l’estimation. On peut se référer par exemple aux slides 60 et suivantes de cette présentation. Globalement, dans le cas d’une proportion, la variance vaut à peu près :
Variance = Proportion * (100% – Proportion) / Taille de l’échantillon
À partir de ce résultat, on peut calculer un intervalle de confiance pour la vraie valeur de la proportion. Il suffit d’enlever et d’ajouter 1,96 fois la racine carrée de la variance. L’intervalle obtenu donne un ensemble de valeurs pour lesquelles l’observation qu’on a, c’est à dire la valeur obtenue sur l’échantillon, n’est pas trop improbable ; on considère ainsi qu’il est possible moins de 5 fois sur 100 pour une vraie valeur hors de cet intervalle d’obtenir un tel résultat.
L’application de ces méthodes ici donne l’intervalle de confiance suivant : [3.1% ; 9.9%]. Il est assez large, car d’une part la taille de l’échantillon est assez faible, et d’autre part la proportion estimée est faible, ce qui a tendance à réduire la précision des estimations : un caractère rare dans une population est difficile à détecter, et n’apparaît pas si souvent dans l’échantillon, donc l’information collectée reste assez faible.
Adaptons le sondage
Même s’il est possible d’être assez déçu par le résultat obtenu à l’aide de ce premier échantillon, il ne faut pas désespérer. En effet, il est toujours possible d’améliorer un plan de sondage une fois que l’on a collecté un peu plus d’informations. Ici, il est possible de faire une remarque générale sur les jeux de mots trouvés : la plupart d’entre eux contiennent soit le mot “Hair”, soit le mot “Tif”. Il est fort probable que l’on trouve plus de jeux de mots dans les salons dont le nom contient un des deux mots que dans la population générale. Nous allons utiliser cette nouvelle information pour réaliser un sondage stratifié (voir ce cours pour plus d’informations).
Pour reprendre l’analyse développée dans la partie précédente, avec une urne remplie de 30 083 boules, il va s’agir ici de séparer a priori, sur un critère connu (qui sera ici la présence ou non du mot “Tif” ou “Hair” dans le nom) les boules entre deux urnes, pour ensuite en tirer un certain nombre dans la première urne puis, indépendamment, un certain nombre (qui peut être différent du premier) dans la seconde urne.
Il ne reste qu’à séparer les 200 salons de coiffure entre les deux catégories, dites strates : la strate 1, qui regroupe les 2 603 salons de coiffure avec “Hair” ou “Tif”, dans laquelle on suppose qu’il y a environ la moitié de jeux de mots, et la strate 2 des autres salons de coiffure, dans laquelle on va supposer qu’il y a 1% de jeux de mots. Ces suppositions permettent de calculer des allocations, c’est à dire le nombre d’unités à tirer dans chaque strate, en utilisant la technique dite de l’allocation de Neyman (slide 61 de cette présentation). Cette allocation, classique en sondages, vise à maximiser la précision de l’estimateur obtenu à la fin, en prenant plus d’individus dans les strates avec une forte variance, ce qui est ici le cas de la strate 1 ; en effet, il y aura à peu près autant de jeux de mots que de non jeux de mots, alors que dans la strate 2 ce sera principalement des noms sans jeu de mots, donc assez peu variés.
Le résultat obtenu ici consiste à tirer 141 salons de coiffure de type 1 et 59 salons de coiffure de type 2. On réalise alors un tel tirage. Les résultats obtenus sont de 68 jeux de mots dans la première strate, et de 1 jeu de mots dans la seconde : “C’est dans l’ère”, assez proche du thème classique de Tif et Hair, mais avec une autre graphie !
Ici, il n’est évidemment pas possible d’extrapoler le résultat à la population totale en disant que la proportion de jeux de mots est de 68+1 sur 200, soit 34.5%. Il faut pondérer les résultats obtenus par la part que représente chacune des strates :
Estimation de la proportion = % de salons dans la strate 1 * proportion de jeux de mots dans la strate 1 + % de salons dans la strate 2 * proportion de jeux de mots dans la strate 2
ce qui donne ici 2603/30083*68/141 + 27480/30083*1/59 = 5,7%. On est bien dans l’intervalle de confiance obtenu tout à l’heure, ce qui est plutôt encourageant. Mais quelle est la précision de ce nouvel estimateur ? Pour cela, on utilise le même type de formule de calcul de variance pour chacune des strates :
Variance_Strate = Proportion_Strate * (100% – Proportion_Strate) / Taille de l’échantillon_Strate
puis on combine ces résultats pour avoir la variance de l’estimation :
Variance = (Part strate 1)² * Variance_Strate_1 + (Part strate 2)² * Variance_Strate_2
et enfin, on construit l’intervalle de confiance de la même façon que précédemment. Nous obtenons ici [4,1% ; 7,3%] qui est plus resserré que celui obtenu au début : nous avons bien amélioré la précision de notre estimation !
Conclusion
Ainsi, en utilisant un sondage intelligent, basé sur l’étude de certaines caractéristiques des jeux de mots dans les salons pour la stratification, nous arrivons au résultat que parmi les 30 083 salons de coiffure, il y en a environ 1 700 dont le nom comporte un jeu de mots, plus ou moins 500, soit très probablement entre 1 200 et 2 200.
Sampling the Twitter graph. Talk at CMStatistics 2015, London.
I will be talking at CMStatistics on Monday, December 14 about how sampling methods can be used to estimate statistics on Twitter’s graph.

![[Sampling] Talk at INSPS – Avignon](https://nc233.com/wp-content/uploads/2016/06/Palais_des_Papes_à_Avignon_-825x510.jpg)
![[Sports] UEFA Euro 2016 predictions – Comments](https://nc233.com/wp-content/uploads/2016/06/UEFA_Euro_2016_qualifying_map.svg_-825x510.png)
![[Sports] UEFA Euro 2016 Predictions – Model](https://nc233.com/wp-content/uploads/2016/06/logo_euro.png)
![[Sampling] Coucher pour réussir ?](https://nc233.com/wp-content/uploads/2016/05/lci_9_mai-825x510.png)
![[Dataviz] Odonymie et couleur politique](https://nc233.com/wp-content/uploads/2016/04/rue_carnot.png)
![[Sports] Don’t miss a shot in biathlon races](https://nc233.com/wp-content/uploads/2016/02/Jeremy_Teela_in_biathlon_-_mens_pursuit_at_2010_Winter_Olympics_2010-02-16_2-825x510.jpg)
![[Sampling] Combien de salons de coiffure ont un jeu de mots dans leur nom ? (Deuxième partie)](https://nc233.com/wp-content/uploads/2016/01/boulet_coiffure.png)
![[Sports] Best/Worst NBA matchups ever](https://nc233.com/wp-content/uploads/2015/12/LosAngeles_Lakers_logo.png)
![[Sampling] Combien de salons de coiffure ont un jeu de mots dans leur nom ? (Première partie)](https://nc233.com/wp-content/uploads/2015/12/Hair_Salon_Stations.jpg)
