Si cette élection présidentielle aura permis quelque chose, c’est bien d’avoir des discussions intéressantes sur les sondages ! Cette course à quatre est inédite dans l’histoire de la Vème République, et avec les grosses surprises de l’actualité récente (Trump et Brexit), il est normal de s’interroger sur l’incertitude réelle contenue dans ces données de sondages. Je propose donc de parler aujourd’hui des “marges d’erreurs” (dits aussi “intervalles de confiance à 95%”) qui ont pour but de quantifier cette incertitude. Je proposerai aussi une idée pour estimer une marge d’erreur prenant en compte à la fois les sondages (“le plan”) et l’évolution du paysage politique (“le modèle”).
Les “marges d’erreur” légales
Commençons par le début : aujourd’hui, on utilise une formule simple pour estimer les marges d’erreur d’un sondage : on prend le chiffre estimé et on effectue +/- deux fois l’erreur-type du sondage aléatoire simple de même taille. Malheureusement, ce mode de calcul ne repose sur aucun socle mathématique. La méthode utilisée par les instituts français, le sondage par quotas est en réalité très éloigné d’un sondage à probabilités égales, et les marges d’erreurs calculées ainsi ne correspondent pas à grand chose. C’est embêtant pour deux raisons qui peuvent sembler contradictoire :
– l’erreur aléatoire du sondage par quotas est probablement plus faible que celle utilisée pour calculer les marges (ce qui a amené des débats sur le “herding”)
– l’erreur totale est sans nul doute plus forte, car elle contient d’autres termes en plus de l’aléatoire (“vote caché”, profils difficiles à joindre, formulation des questions non neutres, etc.)
Le plan et le modèle
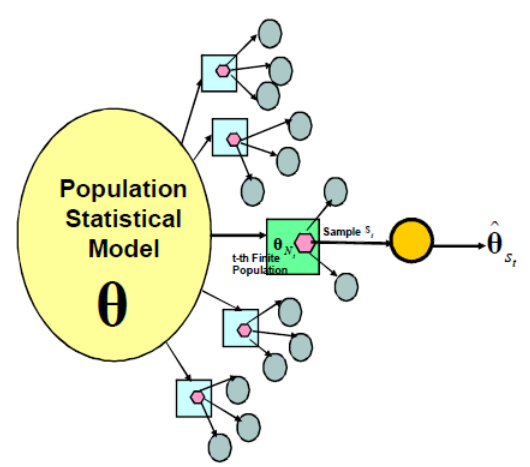
En plus de ces erreurs de mesure, on comprend bien que l’intention de vote sous-jacente des électeurs peut être elle-même variable ! Pour comprendre mieux ce dont on est en train de parler, on peut utiliser la formalisation suivante, empruntée à Binder et Roberts et illustrer avec le sondage politique :
Chaque observation à un instant t des intentions de vote consiste en un sondage en deux phases :
- 1ère phase (modèle) : les intentions de vote des français varient en fonction des événements et du temps. Ce phénomène (supposé aléatoire) produit une population (ou “super-population”) de taille N = 47 millions, le nombre d’inscrits sur les listes électorales.
- 2ème phase (plan) : les sondeurs sélectionnent n personnes de la population (typiquement n = 1000) et mesurent les intentions de vote à l’instant t, avec une certaine erreur de mesure.
Comme le notait récemment Freakonometrics, il est difficile de vraiment séparer les deux phénomènes, et ne prendre en compte que l’erreur d’échantillonnage comme c’est fait aujourd’hui est très peu satisfaisant.
Notez que l’avantage de la formalisation en deux phases choisie ici est que l’on a :
Erreur totale = Erreur modèle + Erreur de sondage
Une idée simple pour estimer ces marges
Pour le deuxième terme, faute de mieux, on va conserver l’erreur de sondage telle qu’elle est calculée aujourd’hui (avec la formule du sondage aléatoire simple) : elle sur-estime l’erreur aléatoire mais ça n’est pas plus mal car cela permet de prendre en compte au moins en partie l’erreur de mesure (voir ce post qui en parle de façon plus détaillée)
Le premier terme est le plus intéressant ! Une idée très simple pour prendre en compte le modèle et l’erreur de sondage : mettre à profit les deuxièmes choix des électeurs, information que l’on retrouve dans un certain nombre d’enquêtes cette année (par exemple chez Ipsos, en page 11 de ce document). L’idée est que si des événements se produisent qui peuvent faire évoluer les intentions de vote, les électeurs auront tendance à se reporter sur leur deuxième choix plutôt que de changer totalement d’avis. Petite remarque : il faut bien intégrer dans ces choix potentiels la possibilité de l’abstention ou du vote blanc, qui ont bien entendu une influence sur la précision des estimations.
Cette idée permettrait d’intégrer la composante modèle à peu de frais ! Reste bien sûr la question de la quantification, mais je me dis que des règles naïves peuvent suffire à obtenir des estimations d’erreur de bonne qualité. Je serais très curieux de savoir si une définition pareille permet de construire des intervalles de confiance avec de bonnes propriétés de couverture. Je crains cependant que les données de deuxième choix des candidats soient peu disponibles pour les présidentielles précédentes.
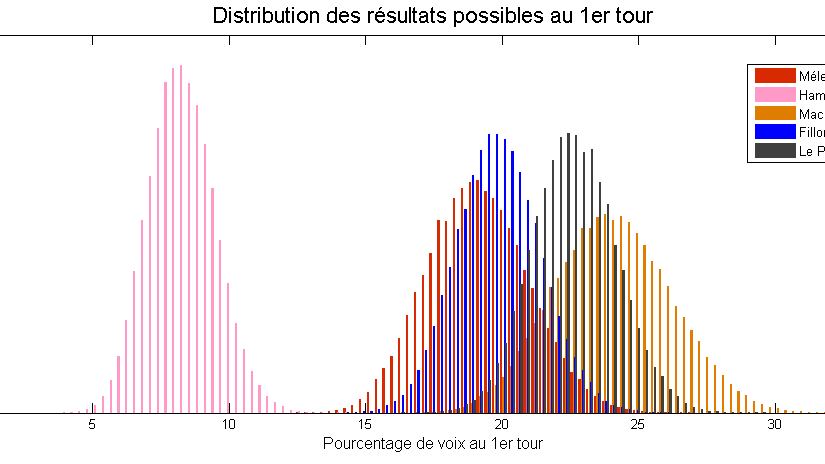
Le modèle de “Too close to call” prend justement en compte ces information, et obtient des marges d’erreur très intéressantes :
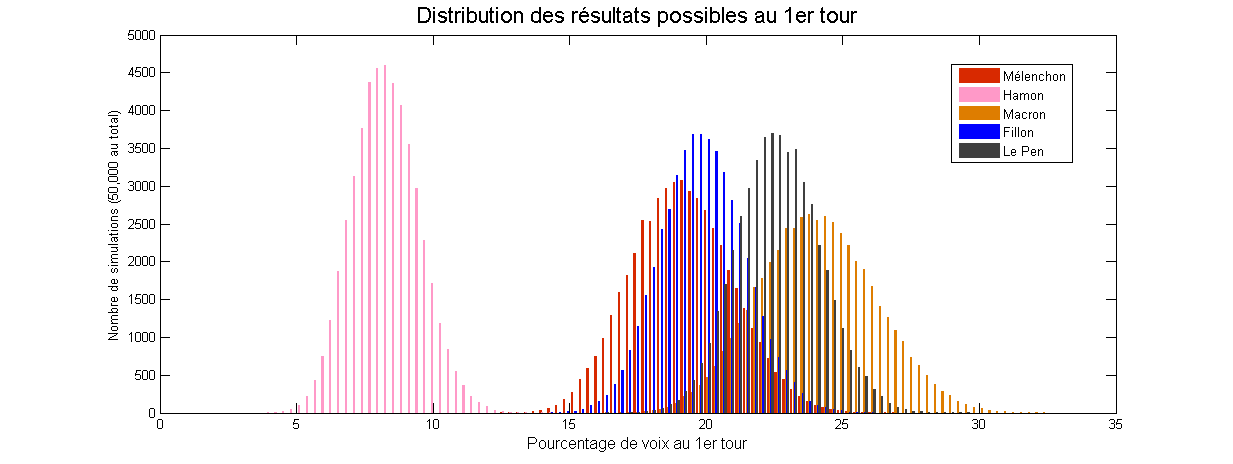
Ces marges reflètent en particulier la relative “sûreté” du score de Marine Le Pen, qui semble posséder une base fidèle ; le score d’Emmanuel Macron semble lui beaucoup plus incertain.

![[12] Le paradoxe d’Alexander](https://nc233.com/wp-content/uploads/2016/12/pokemon-go-capturer-salameche-carapuce-bulbizarre.jpg)
![[Sampling] Coucher pour réussir ?](https://nc233.com/wp-content/uploads/2016/05/lci_9_mai-825x510.png)