Month: September 2015

Disclaimer : I don’t pretend to be a pro rider nor a sport doctor/physiologist, just a data scientist who sometimes likes to apply mathematical modeling to understand some real-world situations 🙂

Are all slopes only for lightweights ?

I’m a bike enthusiast and I used to race (although I was far from being a champion!). I noticed during the training sessions among teammates that had approximately equivalent physical abilities than mine that our ways of performing were very different: every time we climbed a long steep hill, there was no way I could follow their pace no matter how hard I tried, but on the contrary, when I rode in front on a faux plat (especially when there was a lot of wind), I would sometimes find myself a few meters ahead of the pack without really noticing. In fact, I was physically quite different from the rest of the pack: my BMI is roughly equal to 23.5, whereas most of my training mates were in the low 19s.

Watching the pros compete, I found a somewhat similar pattern: although it’s very unlikely that we see a powerful sprinter such as André Greipel win the Flèche Wallonne someday at the famous and feared Wall of Huy ; however, the podium of the 2011 World championships in Copenhaguen was 100% “sprinters”, although the finish line was at the end of a slight slope (with a reasonable gradient of ~ 3%).

The intuition : there exists a “limit gradient”

Based on these two examples, we can see that although very steep hills are obviously lightweight riders’ turf, more powerful (and thus, heavier) riders can still outperform them on slopes with low gradients. So, my intuition was that there exists a “limit gradient” after which the benefits of being powerful (which comes up with being heavier, given that riders have same physical abilities) are overrun by the benefits of being more lightweight, which gives an edge when you have to fight gravity. Are we going to be able to quantify such a limit ?

The power formula

The power needed to move at speed v on a bike is sum of the power needed to move the air, the power needed to resist friction, and the power needed to resist gravity:
\(\begin{align*}
P &= P_{air} + P_{friction} + P_{gravity} \\
&= v \cdot \left( \dfrac{1}{2} \cdot \rho \cdot SC_X \cdot (v-v_{wind})^2 + Mg C_r \cos \phi + C_f (v-v_{wind})^2 + Mg \sin \phi \right) \\
\end{align*}\)
where:
\(\begin{align*}
\rho &= \text{Cubic mass of air} \\
SC_X &= \text{Drag coefficient} \\
C_r &= \text{Wheels coefficient} \\
C_f &= \text{Friction coefficient} \\
M &= \text{total weight rider + bike} \\
g &= 9.81 ms^{-2} \\
\phi &= \text{slope gradient} \\
v_{wind} &= \text{wind speed} \\
\end{align*}\)
The values chosen for the parameters can be found in the R code on my GitHub page.

This formula shows that the lighter you are, the less power you need to move at speed v. But let’s not forget that my hypothesis is precisely that if you are more powerful, you may be heavier but you’ll also be able to produce more power!

W/kg and Kleiber’s law

So now, I need a equation to relate mass and power for riders with similar abilities. One way to do this is to consider that physical abilities are measured by power divided by body mass (a measure that has been widely used and discussed recently). So this is going to be my first work hypothesis:
\(\begin{align*}
\text{H1: } \frac{P}{m} \text{ is constant among riders of the same level}
\end{align*}\)
 

Nevertheless, this doesn’t feel satisfying: sure, it is very common to assume a linear relationship between two parameters, but most of the time we do this because we lack of a better way to describe how things work. And in this case, it seems that power is linked to body weight by Kleiber’s law, which is going to be my second work hypothesis:
\(\begin{align*}
\text{H2: } {\left(\frac{P}{m}\right)}^{0.75} \text{ is constant among riders of the same level}
\end{align*}\)

Plotting the power

Now, I need the value of the constants under hypotheses H1 and H2. For now, I’m only interested in top-level riders, so I choose to use Strava data for Robert Gesink on the wall of Huy to compute the constants under hypotheses H1 and H2. Turns out Gesink, who weighs 70kg, was able to develop a mean power of 557W during the climbing of the hill, which gives us our two constants:
\(\begin{align*}
C_{H1} &= \frac{557}{70} \\
C_{H2} &= {\left( \frac{557}{70} \right)}^{0.75} \\
\end{align*}\)
We are now able to plot the speed advantage that a rider weighing m2 would have over a rider m1 < m2, given that the two riders have similar physical abilities (e.g. same body fat mass). We could plot this function for any m1,m2 but I’m basically looking for a gradient that would equate chances for almost all professional riders, so I’m going to select m1 = 57kg (Joaquim Rodriguez) and m2 = 80kg (André Greipel) from the two most different riders I can think of. We get:

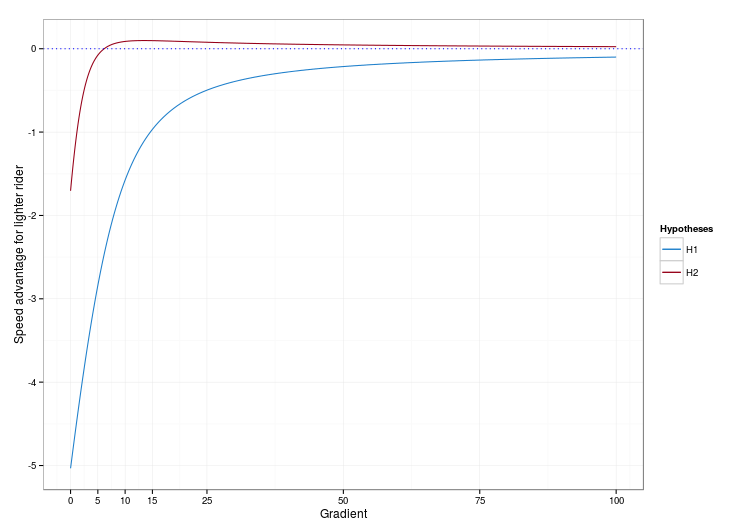
On this graph, we see that under hypothesis H1 (blue curve), the function giving the speed advantage for the lighter rider remains always negative, which means it is always better to be more powerful, even if you have to drag an additional charge while climbing (this is quite surprising, and I think we could use this result to dismiss H1… but a physiologist would qualify way more than me to discuss this particular point!). The curve we get under hypothesis H2 (red curve) is far more interesting. It shows that when the road is flat or faux plat, the more powerful rider has an edge, but for steep slopes (10% and more), the lighter the better. And it between, there exists a “limit gradient”, which confirms what I initially suspected. Yay!

6% : the golden gradient

The “limit gradient” appears to be between 5% and 10%. Now we can write a few lines of code (in R) to determine its exact value. We get:

gradient_lim ~ 6.15 %

According to our model, this means that if a race includes hill whose gradient is approximately 6%, Rodriguez and Greipel stand equal chances of being the fastest (and so probably all the riders in between these very different two champions). In particular, when the finish line of a race is drawn at the top of a climb, it could be really interesting to choose a 6% gradient: below, it would be typically a sprinters-type finish and above, a climbers-type finish. Incidentally, this happens to be roughly the gradient of the final hill of the 2015 World Championships held in Richmond this Sunday! Well done, Virginia!

What about amateurs ?

If I want to do this analysis again for riders of my level, all I need to do is compute the constants according to my Strava data. Turns out on ~1.5 km hills, I can develop approximately 250W, and I weigh 70kg. I get:

gradient_lim ~ 4.9 %

Although it’s not very rigorous, I can confirm that of the (very) few KOMs/not-so-bad-performances I hold on Strava, all of them occurred on slopes with gradients lower than 4%.

Of course, I don’t pretend that the values for the “limit gradients” I find are an exact measure, and always should be the gradient of final hills on every race. For starters, there are a lot of parameters that I didn’t take into account :
– the length of the hill (I voluntarily did not say a word about the fact that different riders could react very differently to hills presenting the same gradient but different lengths)
– that top-level riders may not have exactly the same physical abilities (for example in terms of body fat percentage) when their riding styles are different
– that I’m not sure that Kleiber’s law is really valid in this context? From what I understand, it was primarily designed for evolutionary biology, not for physiology, but I couldn’t find better.
– and of course, that who wins a bike race depends more on the profile of the race before the final sprint, which after all is the very nature of this beautiful sport!

Still, I think we can reasonably assert that in general a 2-3 % gradient is not enough to discourage powerful riders from sprinting, and that a 8-9 % gradient largely favors the Rodriguez-like riders of the pack! And if anyone holds a dataset that could enable me to check this hypothesis, I’d be very happy!