Today, I’d like to write a short note to begin to answer one simple question: which sport is the most conservative? By conservative I mean a sport where the favourite team or athlete wins much more often than the other. As this is quite a large problem, which had been adressed for NFL, I’ll start with some results about some racquet sports, tennis and badminton. I won’t use real data but rather focus on some simulations in order to evaluate the chances to win a match when you’re the #1 tennismen against less talented players.
Game, Set, Match
I won’t explain the rules of scoring in tennis matches, but I’d like to remind you some of the basic principles. To win a tennis match, you need to win 2 or 3 sets. Each set requires you to win at least 6 games, but also two more games than your opponent. And to win a game, you need to score 4 points AND 2 more points than your opponent. These rules mean that a tennis match can last almost forever but as they are very restrictive, they also favor the most efficient player. Let’s have a simple example to understand that.
Let’s say Adam and Becky play a game where they have to score 2 points in 3 rounds. Becky plays way better and has a 90% chance to win each point. The probability of Becky winning is 0.9*0.9 (she wins the first two rounds) + 0.9*0.1*0.9 (she wins round 1, loses round 2 but wins round 3) + 0.1*0.9*0.9 (she loses round 1, but wins rounds 2 and 3), which sums to 97.2%, therefore Adam has a 2.8% chance to win at that game. That is pretty low.
What happens if we add the ‘tennis’ rule of “2 more points than your opponent” ? The game becomes “the first one to score 2 points in a row win”. The maths needed to get Becky’s changes of winning are a little more complex in this example: one way to deal with that problem is to think about the first two rounds. After these two rounds, there is 81% that the winner is Becky, 1% that it is Adam, and 18% that no one has won yet. If we repeat this process, we get a geometric series which sums to approx. 98.8%. Adam’s chances of winning have dropped even more: only 1.2% now!
Let’s go back to Tennis
Now Becky and Adam are tired of playing a game Adam always loses, and they decide to go outside in order to play some tennis. Suppose that Adam is better at this sport than Becky. A conservative hypothesis is to suppose that he’ll win 51% of the time, while she’ll win only 49% of the time. The difference is fairly minor, and that shouldn’t have a big impact, right?
I write a short program in R which simulates thousands of matches in order to know who wins between the two players. The program is quite simple, here is the part about simulating a game :
win_a_point <- function(advantage) {
x = runif(1,0,1)
if (x > advantage) {return(2)}
else {return(1)}
}
gagne_jeu <- function(advantage) {
score = c(0,0)
while ((max(score) < 4) | (abs(score[1]-score[2]) < 2)) {
x = win_a_point(advantage)
score[x] <- score[x] + 1
}
if (score[1] > score[2]) {return(1)}
else {return(2)}
}
The results obtained for 100.000 matches (in 3 winning sets) simulated are compiled in this tabular:
| Point | Game | Set | Match |
| 51% | 52.5% | 58.4% | 63% |
Another interesting result is the following graph:
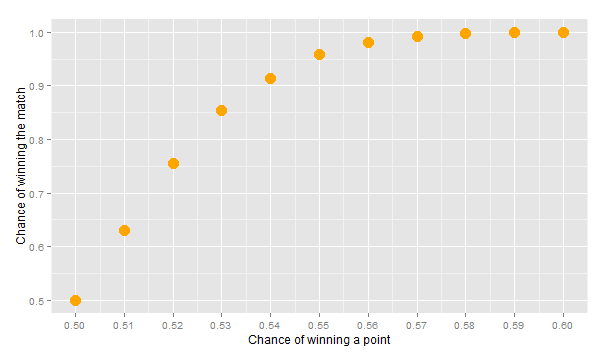
Even if the edge for the better player is as low as 5 percent (55-45 for each point), the match is clearly one-sided. This means that as long as one player have a predominant position and so a little more chance to win each point than his opponent, he is almost assured to win at the end. That makes tennis a very conservative sport!
What about Badminton ?
In order to compare this result to some benchmark, I run the same simulations about Badminton. The rules are quite different but not so much, as it is required to get to 21 points in order to win a game, with at least a two-points lead. Winning a match requires to win two games before your opponent does so. With a small adjustment, I use the same program as before and the results obtained are compiled in this graph:
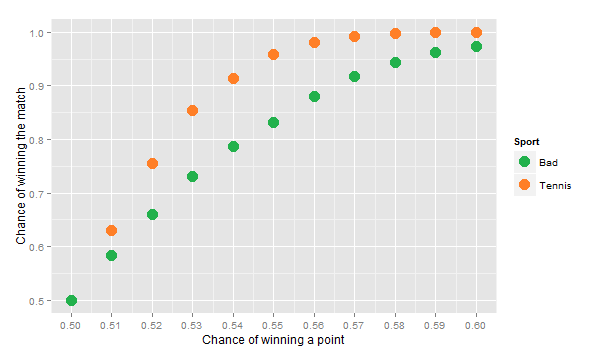
To conclude, compared to Badminton, Tennis is definitely a conservative game!

![[Sports] Why favourite tennismen win even more than they should](https://nc233.com/wp-content/uploads/2015/10/Tennis_Racket_and_Balls-825x510.jpg)