December 2016

[24] Générateur automatique de prénoms

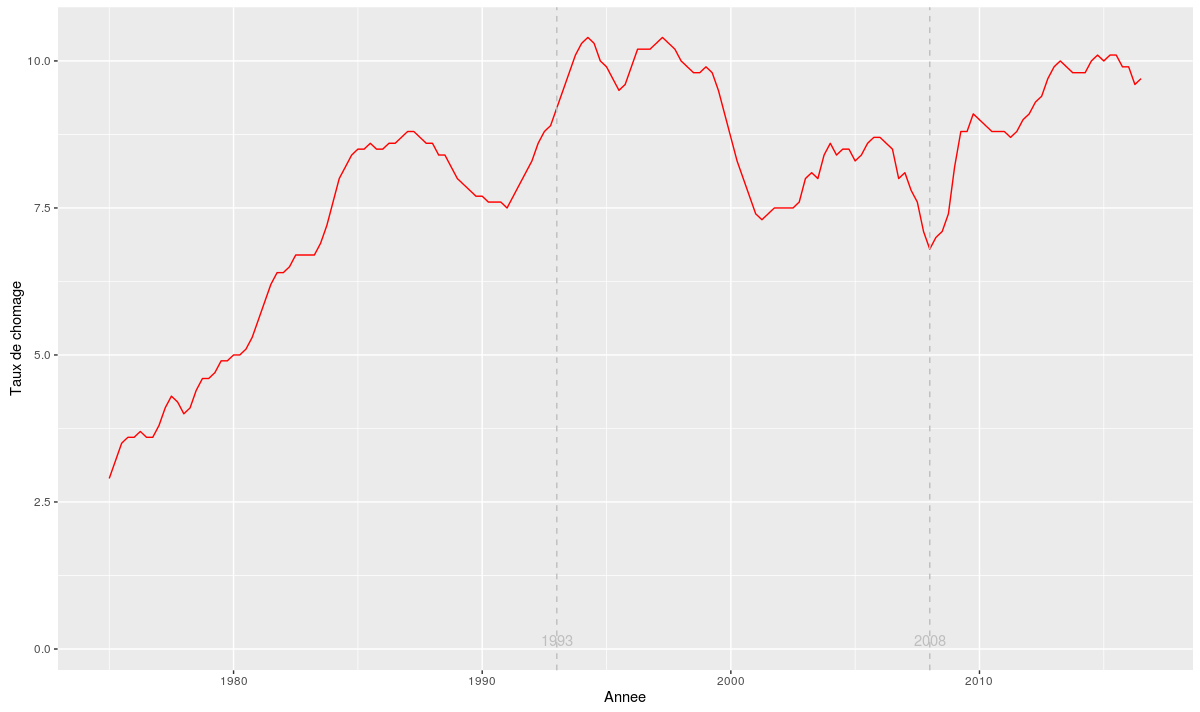
Il est né le divin enfant ! Oui, mais comment va-t-on l’appeler ? Comme nous l’avons remarqué dans un post précédent du calendrier de l’avent, depuis 1993 le choix des prénoms est “libéralisé” en France. Dès lors, pourquoi ne pas chercher de nouveaux prénoms à l’aide d’une méthode mathématique ? Suivant une idée développée dans un excellent post du blog science étonnante, nous avons créé une “machine a inventer des prénoms”, que vous pouvez tester ici :

Mes prénoms préférés générés par la machine pour le moment : Fauliphare et Zauli !

La machine fonctionne a l’aide d’une chaîne de Markov qui indique la probabilité de passage d’une lettre à l’autre. Les probabilités sont calculées à l’aide d’une base de données de prénoms français.

[23] Petite règle statistique pour se représenter une probabilité

Afin de me représenter ce qu’est une probabilité p (particulièrement lorsqu’elle est faible) j’utilise la petite règle suivante :

Si je tente l’expérience 1/p fois (arrondi à l’inférieur lorsque ce n’est pas un nombre entier), j’ai “de bonnes chances” que l’événement se réalise
Il me faudra attendre 3/p essais pour être “pratiquement certain” que l’événement se réalise

Si par exemple on me dit que “un français sur cinq a plus de 65 ans“, je sais qu’en prenant 5 français au hasard dans la population, j’ai de bonnes chances qu’au moins un ait plus de 65 ans parmi eux, et que je suis presque certain d’en trouver un si je sélectionne 15 français.

Il est facile de voir pourquoi ça marche : la probabilité d’obtenir au moins un succès en n lancers est :

\(\Pr(un~succes) = 1-\Pr(aucun~succes)\)

La probabilité de n’avoir aucun succès vérifie une loi binomiale de paramètre p, soit :

\(\Pr(un~succes) = 1-(1-p)^{\frac{1}{p}} = 1 – \exp ( \frac{1}{p} \log(1-p) )\)

Or, quand p est petite, on a:

\(\log(1-p) \sim -p\)

Donc finalement :

\(\Pr(un~succes) \sim 1-\exp(-1) \sim 0.63\)

De la même façon avec 3/p essais :

\(\Pr(un~succes) \sim 1-\exp(-3) \sim 0.95\)

On peut vérifier la qualité des deux approximations avec deux petits graphes (pour p compris entre 0 et 0.5 – au-delà de 0.5, l’arrondi de 1/p étant égal à 1, cela n’aurait plus beaucoup de sens) :

Simulation de l'approximation 1/p pour différentes valeurs de p — Simulation de l’approximation 1/p pour différentes valeurs de p

Simulation de l'approximation 3/p pour différentes valeurs de p — Simulation de l’approximation 3/p pour différentes valeurs de p

Voilà, mis à part quelques effets de seuil et le fait que l’approximation est un peu trop conservative lorsqu’on se rapproche de p = 0.5, ce n’est pas trop mal !

[22] L’affaire “Fun Radio”

Les sondages peuvent parfois faire l’actualité sans parler de politique ! Prenons l’exemple de l’affaire qui oppose Fun Radio et l’institut Médiamétrie, qui est chargé de la mesure d’audience sur les chaînes de télé, de radio, et même des sites internet. Un animateur de la matinale de la radio avait demandé à ses auditeurs, dans le cas où ils seraient contactés par Médiamétrie, de déclarer qu’ils n’écoutaient que Fun Radio (et aucune radio), et qu’ils étaient à l’écoute de la station durant toute la journée. Cela a conduit Médiamétrie à retirer momentanément Fun Radio du panel de mesure. Cette décision a eu des conséquences importantes sur les finances de la radio : en effet, la répartition des revenus publicitaires est directement indexée sur ces calculs d’audience. Ainsi, la radio s’est pourvu en justice pour être réintégrée, ce qui sera a priori le cas.

Je ne commenterai pas la décision de justice, n’y connaissant rien, mais j’ai plutôt envie de commenter d’un point de vue de sondeur cette affaire. En effet, si l’on résume, les messages ont eu (potentiellement) trois effets :

Encourager les auditeurs de la matinale à répondre aux enquêteurs de Médiamétrie lorsque ceux-ci les contactent ;
Sur-déclarer un temps d’écoute pour la radio Fun Radio ;
Sous-déclarer un temps d’écoute pour d’autres radios.

À mon sens, ces trois problèmes demandent des solutions différentes ! Je vais laisser le premier de coté, qui me semble le plus intéressant d’un point de vue sondages, pour parler brièvement des deux autres.

Tout d’abord le deuxième : on peut imaginer qu’en utilisant des sources extérieures comme le panel Radio global sur le temps d’écoute moyen de la radio en France, ou des enquêtes type Emploi du Temps de l’INSEE, on puisse repérer des outliers (c’est à dire des personnes qui déclarent des valeurs qui sortent très largement de la moyenne) et les traiter, ou les exclure. En gros, écouter la radio 24h par jour, c’est suspect.

Le troisième point est le plus ardu à corriger, mais on peut faire l’hypothèse (soyons optimistes) que quelqu’un qui est prêt à mentir si un animateur radio le lui demande est un auditeur exclusif de la radio en question, ce qui neutralise l’effet.

Reste donc le premier point. Tout praticien des sondages sait que les individus sélectionnés dans un échantillon ne sont pas tous volontaires pour répondre aux questionnaires, loin de là. Cela crée un biais, qui est étudié et traité en statistiques par des méthodes de “correction de la non-réponse”. On pourrait donc imaginer que ces méthodes servant à prendre en compte la non-réponse pourraient suffire à annuler le biais en question, mais le problème est plus compliqué que cela. Je vais tenter d’expliquer à l’aide d’un exemple : supposons qu’il existe uniquement deux radios, une pour les “jeunes”, et une pour les autres. Dans ce cas, Médiamétrie cherche à savoir combien de personnes écoutent chaque radio. Si 10% des jeunes répondent avant l’effet de l’annonce, Médiamétrie a l’habitude de multiplier par 10 (pour simplifier) le nombre d’auditeurs de Fun Radio : si le nombre de répondants augmente, il suffit de changer un peu le coefficient multiplicatif, mais cela n’aura pas d’effet sur l’écoute de l’autre radio, et les chiffres devraient être globalement les mêmes.

Pourquoi je dis que c’est plus compliqué ? Parce que les méthodes de la correction de la non-réponse reposent sur de l’information auxiliaire, par exemple les informations démographiques. On peut facilement séparer (par exemple via les variables d’âge) l’auditeur moyen de Fun Radio de celui de France Inter, mais ce sera plus compliqué avec NRJ ou une autre station destinée à un même public. Il est d’ailleurs intéressant de noter que c’est NRJ qui a initialement porté réclamation auprès de Médiamétrie. Et donc, la mesure “absolue” de l’audience de Fun Radio (en excluant les points 2 et 3) n’est pas trop mauvaise. Celle de Nostalgie n’est pas impactée non plus, mais celle de NRJ peut l’être énormément. En effet, plus de jeunes répondent, mais les répondants écoutent moins NRJ (car ils sont plutôt auditeurs de Fun Radio), donc l’estimation finale est à la baisse pour cette radio, alors que le comportement de leurs auditeurs n’a pas changé.

Voilà, vous en savez plus sur ceux qui travaillent en secret pour Médiamétrie !

[21] Lettres internationales

Reprenons la même logique que dans l’article du 16 décembre : quelle lettre a le plus d’habitants dans le Monde ? Ce coup-ci, on va se limiter au nom des pays (encore que ce serait intéressant de reproduire l’idée sur les villes, mais les données seraient difficiles à trouver : peut-être une prochaine fois !). Pour cela, on utilise les données disponibles ici, on normalise les noms des pays en retirant tout ce qui est entre parenthèses et précédé d’une virgule (décision totalement subjective, mais ce n’est pas une science exacte). Les noms des pays sont ici en Anglais : c’est la norme internationale après tout.

Les résultats sont les suivants :

Les lettres des deux pays les plus peuplés ont été colorées en bleu pour la Chine, en jaune pour l’Inde, et en vert pour les trois lettres que les pays ont en commun (encore une fois, en anglais). On remarque que ces trois lettres, I, N et A, sont les trois plus fréquentes : est-ce que c’est dû à leur appartenance à ces deux pays, ou est-ce que c’est le fait qu’elles soient fréquentes qui fait qu’elles se retrouvent dans les deux noms ?

Pour rappel, les résultats obtenus sur les villes de France sont les suivants :

On voit bien que la répartition n’est pas la même : E, R, S par exemple sont bien moins fréquentes au niveau mondial qu’au niveau français.

[20] Données du chômage au format “xkcd”

Aujourd’hui on reprend les données du chômage récupérées hier sur le site de l’Insee. On va transformer le graphe qu’on a créé avec ggplot2 pour le faire ressembler aux graphes de l’excellent comic xkcd. On va utiliser pour cela le package R xkcd :

install.packages("xkcd", dependencies = T)

Il faut ensuite installer la police “xkcd”. Le script suivant fait l’affaire :

library(extrafont)

download.file("http://simonsoftware.se/other/xkcd.ttf",
 dest="xkcd.ttf", mode="wb")
system("mkdir ~/.fonts")
system("cp xkcd.ttf ~/.fonts")
font_import(pattern = "[X/x]kcd", prompt=FALSE)
fonts()
fonttable()
if(.Platform$OS.type != "unix") {
 ## Register fonts for Windows bitmap output
 loadfonts(device="win")
} else {
 loadfonts()
}

Il ne reste plus qu’à modifier un peu notre graphe original et utiliser le thème theme_xkcd() dans ggplot2. Notez l’utilisation de geom_smooth à la place de geom_line afin de lisser la courbe pour renforcer l’aspect bande dessinée.

library(xkcd)
library(ggplot2)

plot_chomage <- ggplot(donnees_chomage, aes(x=TIME_PERIOD, y=OBS_VALUE)) +
 geom_smooth(colour="red", size=2, level=0, formula = y ~ poly(x, 9), method="lm") +
 xlab("Annee") +
 ylab("Taux de chomage") +
 geom_vline(xintercept = c(1993,2008), color="grey", linetype="dashed") +
 annotate("text", c(1993,2008), c(0.15), label=c("1993","2008"), 
 color="grey", family="xkcd") +
 theme_xkcd()

print(plot_chomage)

Taux de chômage en France entre 1975 et 2016 – style “xkcd”

Et voilà un graphe au style “xkcd” pour le taux de chômage en France ! Le sujet n’étant peut-être pas le plus adapté au format BD, je donne pour l’exemple le graphe des prénoms de l’article du 13 décembre que je me suis également amusé à xkcd-iser :

Part des 10 prénoms les plus populaires en France - style xkcd — Part des 10 prénoms les plus populaires en France – style xkcd

[19] Données du chômage avec R et SDMX-ML

Aujourd’hui un petit post un peu plus “pratique”. On va réaliser le graphique du taux de chômage en France depuis 1975 en utilisant R. Les données sont disponibles sur le site de l’INSEE. En suivant ce lien on va pouvoir les télécharger au format csv. Mais il est beaucoup plus sympathique d’utiliser une méthode un peu plus automatique pour récupérer ces données. Ainsi, dès que l’INSEE les mettra à jour (le trimestre prochain par exemple), il suffira de relancer le script R et le graphe se mettra automatiquement à jour.

Pour ce faire, on va utiliser la compatibilité du nouveau site de l’Insee avec la norme SDMX. Le package R rsdmx va nous permettre de récupérer facilement les données en utilisant cette fonctionnalité :

install.packages("rsdmx")
library(rsdmx)

Sur la page correspondant aux données sur le site de l’Insee, on récupère l’identifiant associé : 001688526. Cela permet de construire l’adresse à laquelle on va pouvoir demander à rsdmx de récupérer les données : http://www.bdm.insee.fr/series/sdmx/data/SERIES_BDM/001688526. On peut également ajouter des paramètres supplémentaires en les ajoutant à la suite de l’url (en les séparant par un “?”). On utilise ensuite cette adresse avec la fonction readSDMX:

url_chomage_insee <- "http://www.bdm.insee.fr/series/sdmx/data/SERIES_BDM/001688526?periodeDebut=1&anneeDebut=1975&periodeFin=3&anneeFin=2016&recherche=criteres&codeGroupe=1533"
donnees_chomage_sdmx <- readSDMX(url_chomage_insee)
donnees_chomage <- as.data.frame(donnees_chomage_sdmx)

On peut regarder la structure des données que l’on a à ce stade :

> str(donnees_chomage)
'data.frame':	167 obs. of  12 variables:
 $ IDBANK          : Factor w/ 1 level "001688526": 1 1 1 1 1 1 1 1 1 1 ...
 $ FREQ            : Factor w/ 1 level "T": 1 1 1 1 1 1 1 1 1 1 ...
 $ TITLE           : Factor w/ 1 level "Taux de chômage au sens du BIT - Ensemble - France métropolitaine - Données CVS": 1 1 1 1 1 1 1 1 1 1 ...
 $ LAST_UPDATE     : Factor w/ 1 level "2016-11-17": 1 1 1 1 1 1 1 1 1 1 ...
 $ UNIT_MEASURE    : Factor w/ 1 level "PCT": 1 1 1 1 1 1 1 1 1 1 ...
 $ UNIT_MULT       : Factor w/ 1 level "0": 1 1 1 1 1 1 1 1 1 1 ...
 $ REF_AREA        : Factor w/ 1 level "FM": 1 1 1 1 1 1 1 1 1 1 ...
 $ DECIMALS        : Factor w/ 1 level "1": 1 1 1 1 1 1 1 1 1 1 ...
 $ TIME_PER_COLLECT: Factor w/ 1 level "PERIODE": 1 1 1 1 1 1 1 1 1 1 ...
 $ TIME_PERIOD     : chr  "2016-Q3" "2016-Q2" "2016-Q1" "2015-Q4" ...
 $ OBS_VALUE       : chr  "9.7" "9.6" "9.9" "9.9" ...
 $ OBS_STATUS      : chr  "P" "A" "A" "A" ...

Les deux colonnes qui vont nous intéresser sont “TIME_PERIOD” (date de la mesure) et “OBS_VALUE” (taux de chômage estimé). Pour le moment, ces données sont au format “caractère”. On va les transformer respectivement en “date” et en “numérique”. Notez que l’intégration du trimestre nécessite de passer par le package “zoo” (pour la fonction as.yearqtr) :

library(zoo)

donnees_chomage$OBS_VALUE <- as.numeric(donnees_chomage$OBS_VALUE)

donnees_chomage$TIME_PERIOD <- as.yearqtr(donnees_chomage$TIME_PERIOD, format = "%Y-Q%q")

Il ne reste plus qu’à utiliser l’excellent package ggplot2 pour créer le graphe. On en profite pour ajouter des lignes verticales en 1993 et 2008 (dates des deux dernières crises économiques majeures) :

library(ggplot2)
 
plot_chomage <- ggplot(donnees_chomage, aes(x=TIME_PERIOD, y=OBS_VALUE)) +
 geom_line(colour="red") +
 xlab("Annee") +
 ylab("Taux de chomage") +
 geom_vline(xintercept = c(1993,2008), color="grey", linetype="dashed") +
 annotate("text", c(1993,2008), c(0.15), label=c("1993","2008"), 
 color="grey")

print(plot_chomage)

Taux de chômage en France entre 1975 et 2016

Rendez-vous demain pour un article où on s’amusera à faire ressembler ce graphe à ceux du comic xkcd.

[18] Recensement et constitution américaine

C’est l’avent, sans nul doute la meilleure période pour faire un petit post sur le recensement.

Le principe du recensement

Un recensement consiste à établir un registre de toutes les personnes vivant dans un pays. Le principe en est même inscrit dans l’article 1 de la constitution américaine. Le gouvernement américain est ainsi tenu de dénombrer régulièrement le nombre de ses citoyens, afin notamment d’ajuster le nombre de représentants de chaque Etat dans les différentes institutions démocratiques, entre autres, le sénat, la chambre des représentants et le collège électoral.

Recensement en Alaska en 1940. Source : https://en.wikipedia.org/wiki/United_States_Census#/media/File:1940_Census_-_Fairbanks,_Alaska.jpg — Recensement en Alaska en 1940. By Dwight Hammack, U.S. Bureau of the Census

Recenser toute la population d’un pays est bien entendu long et coûteux. C’est pourquoi historiquement, ces opérations n’étaient conduites qu’à certains moments (une fois tous les 7 ans en moyenne en France aux XIXe et XXe siècles). Un des inconvénients de cette façon de procéder est que le dernier recensement disponible à date peut présenter une information un peu datée ! Si les évolutions démographiques sont rapides, le données d’un recensement effectué plusieurs années auparavant ne refléteront pas la réalité.

Introduction d’une petite partie de sondages

Ainsi, dans le courant des années 2000, quelques instituts nationaux de statistiques ont introduit une petite part de sondage dans leur recensement. L’idée est de ne plus effectuer un dénombrement complètement exhaustif, mais d’effectuer un sondage avec un taux assez fort dans certaines zones géographiques. Ceci à la fois pour gagner en coûts, corriger certains biais de la méthode exhaustive, et surtout permettre d’effectuer le recensement plus souvent, c’est-à-dire de donner aux statisticiens des informations plus récentes !

En France, cette petite part de sondage a été combinée avec un recensement tournant. Les communes de moins de 10000 habitants sont entièrement recensées tous les cinq ans, par roulement, alors que les communes de plus de 10000 habitants ne voient chaque année qu’une fraction (8%) de leur population recensée (plus de détails ici).

L’utilisation du recensement pour la répartition des représentants

Aux Etats-Unis, le Census Bureau fait partie de ces instituts nationaux de statistiques qui ont décidé d’ajouter une petite part de théorie statistique à leur recensement. Mais la cour Suprême semble sceptique quant à l’utilisation de telles méthodes “inexactes”. En 1999, elle a décidé que les résultats du recensement qui auront été obtenus en utilisant la méthode par sondage ne pourraient pas être utilisées pour “l’apportionment“, c’est-à-dire la constitution des institutions démocratiques représentatives.

Le Census Bureau collecte quand même des données par cette méthode car elles sont utiles dans beaucoup de domaines (par exemple cet article très intéressant sur lequel je reviendrai un de ces jours). Mais elles ne seront pas utilisées pour calculer le nombre de représentants au Sénat, à la chambre ou dans le collège électoral.

Notons que certains statisticiens pensent que le recensement “exhaustif” américain est biaisé en défaveur des minorités, ce qui fait écho aux débats récents sur la constitution du collège électoral.

Le découpage électoral en France

Circonscriptions électorales élections législatives 2012. Source : http://www.lefigaro.fr/politique/2009/07/28/01002-20090728ARTFIG00458-la-nouvelle-carte-electorale-pour-2012-.php

En France, la délimitation des circonscriptions législatives se nomme le découpage électoral. La dernière modification de ces circonscriptions a été effectuée en 2010 en utilisant les données démographiques du recensement de la population 2009. Autrement dit, notre mode de découpage des circonscriptions utilisant cette méthode de recensement serait considéré… inconstitutionnel aux Etats-Unis !

[17] Avenue, Rue ou Boulevard Jean Jaurès ?

Petit retour dans le monde de l’odonymie, après l’article de mercredi dernier, et celui plus ancien où nous vous proposions de regarder de quelle couleur politique était votre rue !

Nous allons nous intéresser aux types de voie qui sont associés aux différentes personnalités. Pour cela, nous avons sélectionné les 20 personnalités qui ressortent le plus dans les noms de voirie en France, et nous avons compté pour chaque type de voie (rue, avenue, allée, etc.) avec quelle fréquence ce nom était présent. Les résultats sont résumés par le tableau suivant, coloré à l’aide d’Excel :

On remarque plusieurs résultats intéressants :

Ce sont les avenues qui sont les plus fréquentes, en tout cas celles relatives à ces personnalités. Cela peut s’expliquer facilement : ce sont souvent de grandes artères et il est classique de les nommer en honneur de personnalités très célèbres.
Les rues et places sont très souvent associées à des personnalités militaires ou politiques, surtout le Général de Gaulle et dans une moindre mesure Clemenceau et le Général Leclerc.
À l’inverse, les impasses et les allées sont plus souvent associés à des personnalités du monde littéraire ou artistique, comme Émile Zola, Georges Brassens ou Jean de la Fontaine.

[16] Lettres de France

On va répondre aujourd’hui à une question que personne ne s’est jamais posé : quelle lettre a le plus d’habitants en France ? C’est à dire que par exemple pour la lettre A, on regarde toutes les communes françaises qui possèdent un A, et l’on cherche à savoir quelle partie de la population cela représente. Pour cela, on va utiliser deux choses qui ont l’air simples mais qui ne le sont pas :

Les données des populations légales, qui sont un des produits les plus importants de l’INSEE, mais qui sont très dures à trouver sur leur site : elles sont ici. Ouf.
Les expressions régulières, qui vont permettre ici de retrouver tous les noms de communes dans lesquels il y a une lettre. Ici, on va utiliser la fonction grepl de R pour faire cela. Si ça vous intéresse, un petit jeu ici.

Les résultats sont les suivants :

On a coloré en bleu les lettres de la capitale, Paris. Malgré ses deux millions et demi d’habitants, cela ne suffit pas à faire de toutes ses lettres les plus peuplées de France : rien ne dépasse le “E”.

[15] Fuseaux horaires européens

La construction de l’Union Européenne est un projet datant de la fin de la Seconde Guerre Mondiale. Cependant, on ne se pose pas toujours les bonnes questions à son sujet : comment faire pour mettre tout le monde dans une même pièce pour discuter si nous n’avons pas tous la même heure ? Concrètement, et en négligeant les parties hors Europe des pays de l’Union, il y a trois fuseaux horaires différents en Europe :

L’heure d’Europe de l’Ouest (WET), par exemple au Royaume-Uni (qu’on compte toujours avec nous, tant que le Brexit n’est pas acté).
L’heure d’Europe Centrale (CET), par exemple en France.
L’heure d’Europe de l’Est (EET), par exemple en Grèce.

Nous n’avons donc pas tous la même heure. Mais quelle est la probabilité, si l’on choisit deux européens au hasard, que leurs montres indiquent la même heure (en admettant qu’elles soient suisses et donc parfaitement réglées) ? Pour cela, nous avons besoin de données sur la population des différents pays européens, disponibles sur le site de l’INED. On calcule ensuite le tableau suivant, qui résume la probabilité des “couples” de fuseaux horaires obtenus par notre tirage au hasard :

	WET	CET	EET
WET	2,5 %	11,7 %	1,6 %
CET	11,7 %	55,4 %	7,3 %
EET	1,6 %	7,3 %	1 %

Pour répondre à notre question initiale, il suffit de sommer les cases en gras du tableau : nous avons donc 58,8 % de chances que les deux personnes aient bien la même heure à leur montre. Ou sur leur téléphone portable, plus probablement.

Si l’on compare aux États-Unis, pour lesquels les données sont disponibles ici, on trouve que deux américains ont la même heure dans seulement 34,7% des cas. Cela ne devrait pas être si compliqué que ça de se mettre d’accord ?