Afin de me représenter ce qu’est une probabilité p (particulièrement lorsqu’elle est faible) j’utilise la petite règle suivante :
- Si je tente l’expérience 1/p fois (arrondi à l’inférieur lorsque ce n’est pas un nombre entier), j’ai “de bonnes chances” que l’événement se réalise
- Il me faudra attendre 3/p essais pour être “pratiquement certain” que l’événement se réalise
Si par exemple on me dit que “un français sur cinq a plus de 65 ans“, je sais qu’en prenant 5 français au hasard dans la population, j’ai de bonnes chances qu’au moins un ait plus de 65 ans parmi eux, et que je suis presque certain d’en trouver un si je sélectionne 15 français.
Il est facile de voir pourquoi ça marche : la probabilité d’obtenir au moins un succès en n lancers est :
\(\Pr(un~succes) = 1-\Pr(aucun~succes)\)La probabilité de n’avoir aucun succès vérifie une loi binomiale de paramètre p, soit :
\(\Pr(un~succes) = 1-(1-p)^{\frac{1}{p}} = 1 – \exp ( \frac{1}{p} \log(1-p) )\)Or, quand p est petite, on a:
\(\log(1-p) \sim -p\)Donc finalement :
\(\Pr(un~succes) \sim 1-\exp(-1) \sim 0.63\)De la même façon avec 3/p essais :
\(\Pr(un~succes) \sim 1-\exp(-3) \sim 0.95\)
On peut vérifier la qualité des deux approximations avec deux petits graphes (pour p compris entre 0 et 0.5 – au-delà de 0.5, l’arrondi de 1/p étant égal à 1, cela n’aurait plus beaucoup de sens) :
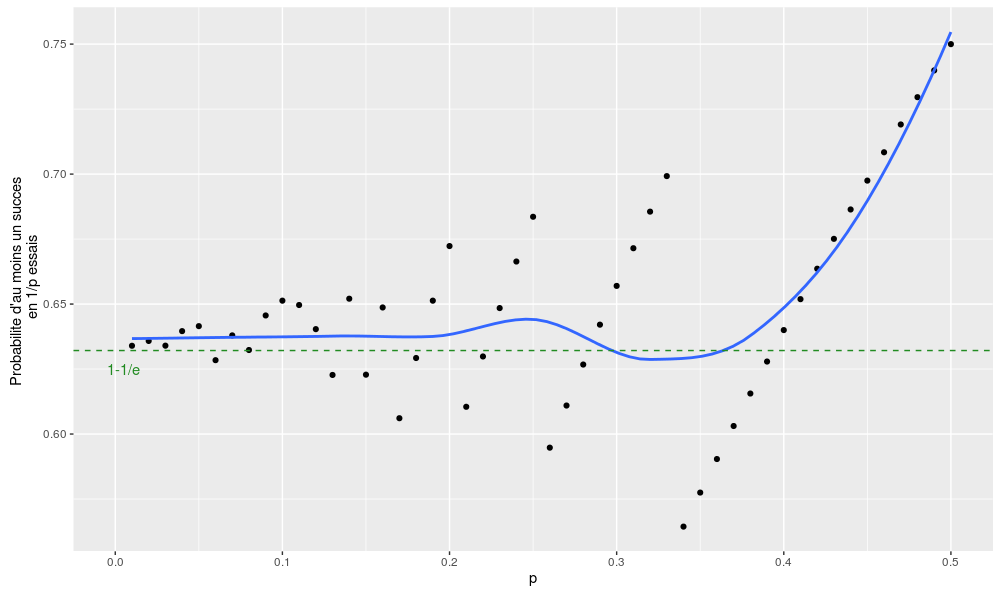
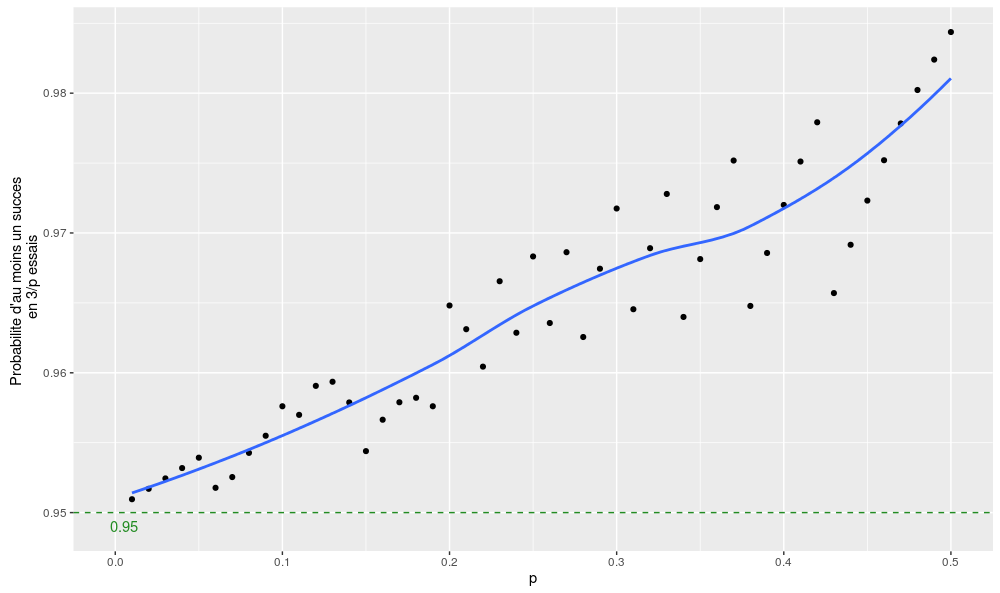
Voilà, mis à part quelques effets de seuil et le fait que l’approximation est un peu trop conservative lorsqu’on se rapproche de p = 0.5, ce n’est pas trop mal !