Antoine Rebecq – Page 3

[18] Recensement et constitution américaine

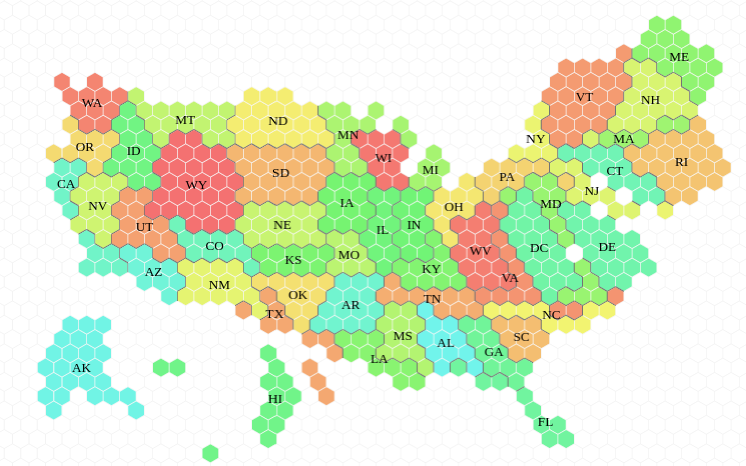
C’est l’avent, sans nul doute la meilleure période pour faire un petit post sur le recensement.

Le principe du recensement

Un recensement consiste à établir un registre de toutes les personnes vivant dans un pays. Le principe en est même inscrit dans l’article 1 de la constitution américaine. Le gouvernement américain est ainsi tenu de dénombrer régulièrement le nombre de ses citoyens, afin notamment d’ajuster le nombre de représentants de chaque Etat dans les différentes institutions démocratiques, entre autres, le sénat, la chambre des représentants et le collège électoral.

Recensement en Alaska en 1940. Source : https://en.wikipedia.org/wiki/United_States_Census#/media/File:1940_Census_-_Fairbanks,_Alaska.jpg — Recensement en Alaska en 1940. By Dwight Hammack, U.S. Bureau of the Census

Recenser toute la population d’un pays est bien entendu long et coûteux. C’est pourquoi historiquement, ces opérations n’étaient conduites qu’à certains moments (une fois tous les 7 ans en moyenne en France aux XIXe et XXe siècles). Un des inconvénients de cette façon de procéder est que le dernier recensement disponible à date peut présenter une information un peu datée ! Si les évolutions démographiques sont rapides, le données d’un recensement effectué plusieurs années auparavant ne refléteront pas la réalité.

Introduction d’une petite partie de sondages

Ainsi, dans le courant des années 2000, quelques instituts nationaux de statistiques ont introduit une petite part de sondage dans leur recensement. L’idée est de ne plus effectuer un dénombrement complètement exhaustif, mais d’effectuer un sondage avec un taux assez fort dans certaines zones géographiques. Ceci à la fois pour gagner en coûts, corriger certains biais de la méthode exhaustive, et surtout permettre d’effectuer le recensement plus souvent, c’est-à-dire de donner aux statisticiens des informations plus récentes !

En France, cette petite part de sondage a été combinée avec un recensement tournant. Les communes de moins de 10000 habitants sont entièrement recensées tous les cinq ans, par roulement, alors que les communes de plus de 10000 habitants ne voient chaque année qu’une fraction (8%) de leur population recensée (plus de détails ici).

L’utilisation du recensement pour la répartition des représentants

Aux Etats-Unis, le Census Bureau fait partie de ces instituts nationaux de statistiques qui ont décidé d’ajouter une petite part de théorie statistique à leur recensement. Mais la cour Suprême semble sceptique quant à l’utilisation de telles méthodes “inexactes”. En 1999, elle a décidé que les résultats du recensement qui auront été obtenus en utilisant la méthode par sondage ne pourraient pas être utilisées pour “l’apportionment“, c’est-à-dire la constitution des institutions démocratiques représentatives.

Le Census Bureau collecte quand même des données par cette méthode car elles sont utiles dans beaucoup de domaines (par exemple cet article très intéressant sur lequel je reviendrai un de ces jours). Mais elles ne seront pas utilisées pour calculer le nombre de représentants au Sénat, à la chambre ou dans le collège électoral.

Notons que certains statisticiens pensent que le recensement “exhaustif” américain est biaisé en défaveur des minorités, ce qui fait écho aux débats récents sur la constitution du collège électoral.

Le découpage électoral en France

Circonscriptions électorales élections législatives 2012. Source : http://www.lefigaro.fr/politique/2009/07/28/01002-20090728ARTFIG00458-la-nouvelle-carte-electorale-pour-2012-.php

En France, la délimitation des circonscriptions législatives se nomme le découpage électoral. La dernière modification de ces circonscriptions a été effectuée en 2010 en utilisant les données démographiques du recensement de la population 2009. Autrement dit, notre mode de découpage des circonscriptions utilisant cette méthode de recensement serait considéré… inconstitutionnel aux Etats-Unis !

[13] Prénoms : part du top 10 et diversification

Avec chaque nouvelle année vient sa liste des prénoms tendance. Je suis toujours étonné de constater que beaucoup d’enfants possèdent des prénoms peu portés. Je me suis demandé si mon ressenti était exact, et le cas échéant si la tendance était récente. J’ai utilisé pour cela le fichier des prénoms de l’INSEE de 1946 à 2006, et fait un graphe de la part dans le total des 10 prénoms les plus populaires de chaque année :

Part du total pour les 10 prénoms les plus populaires donnés par année. Lecture : en 1960, les 10 prénoms les plus populaires représentaient 40% du total des naissances

Mis à part une hausse de la courbe (donc une baisse de la diversité) des prénoms féminins dans les années soixante, la tendance est bien à la baisse. La loi de 1993 qui libéralise le choix des prénoms ne semble d’ailleurs pas avoir eu d’effet sur cette tendance. En conséquence, j’imagine qu’il y a bien moins de doublons dans les classes qu’il ne pouvait y en avoir il y a quelques années.

[12] Le paradoxe d’Alexander

Il paraît que tout mathématicien apprécie un bon paradoxe. Et il semblerait aussi qu’il n’y ait pas de bon blog de maths sans paradoxe, comme nous le prouvent par exemple Freakonometrics, Science étonnante ou encore la chaîne youtube Science4All ! Donc aujourd’hui on inaugure la section paradoxe de ce blog avec un petit problème dû à Alexander (1989).

Imaginez une tombola où il y a n = 3 prix distribués. Une même personne ne pourra recevoir qu’un seul prix, mais il n’y a pas de limite dans le nombre de tickets que chacun peut acheter pour maximiser ses chances de remporter un lot. Le tirage se déroule comme suit : on met tous les tickets dans l’urne et on tire le gagnant du premier lot. Si la personne tirée possédait plusieurs tickets, on les retire tous de l’urne, et on recommence jusqu’à ce que les trois prix aient été attribués.

Obtenir un de ces prix vous tient très à cœur et vous achetez 225 000 tickets de loterie ! Votre éternel rival (noté R) lui aussi veut un de ces lots à tout prix et achète également 225 000 tickets. 50 000 autres personnes ont joué à la loterie, mais elles n’ont acheté qu’un seul ticket chacune.

Vous manquez malheureusement le tirage mais vous croisez votre rival qui en sort, tout dépité. Logiquement, vous devriez vous réjouir, non ? Le fait qu’il n’ait pas gagné malgré ses 225 000 tickets devrait vous donner mécaniquement plus de chances. En termes plus mathématiques, on devrait donc avoir :

$\Pr(vous~perdez~|~R~a~perdu) \leq \Pr(vous~perdez)$

On peut très simplement faire des simulations de cette loterie en R (et avec l’aide du package foreach, que j’apprécie beaucoup). On va faire 100000 simulations parce que la différence entre les deux probabilités n’est pas très élevée :

library(foreach)


N <- 500000
multiTickets <- 225000

id_self <- 1
id_rival <- 2
pop <- c(rep(1,multiTickets),rep(2,multiTickets),3:(N-2*multiTickets))

n <- 3

nSim <- 100000

successive_sample <- function(pop, n) {
 
 sample_set <- rep(0,n)
 popTemp <- pop
 k <- 1 ## temp size of sample
 
 cont <- TRUE
 
 while(cont) {
 
 drawn_unit <- sample(popTemp,1)
 sample_set[k] <- drawn_unit
 k <- k+1
 popTemp <- popTemp[popTemp != drawn_unit]
 
 if( k > n ) {
 cont <- FALSE
 }
 
 }
 
 return(sample_set)
}

sim_lottery <- foreach(k = 1:nSim, .combine=rbind) %do% {
 successive_sample(pop, n)
}


p_lost <- sum(as.numeric(
 apply(sim_lottery,1, function(x) { return(!(id_self %in% x)) } )
)) / nSim

sim_rival_lost <- sim_lottery[apply(sim_lottery,1,function(x) { return(!(id_rival %in% x)) }),]
p_lost_conditional <- sum(as.numeric(
 apply(sim_rival_lost,1,
 function(x) { return(!(id_self %in% x)) })
)) / nrow(sim_rival_lost)

Et on observe :

> p_lost
[1] 0.02871
> p_lost_conditional
[1] 0.03449465

C’est-à-dire :

$\Pr(vous~perdez~|~R~a~perdu) > \Pr(vous~perdez)$

Donc contrairement à notre intuition, le fait de savoir que notre rival a perdu ne doit pas nous réjouir, car nous avons maintenant moins de chances de gagner que sans cette information !

Plutôt rigolo, non ? Vous pouvez essayer de faire tourner le code précédent avec des allocations en tickets un peu moins “bizarres”. Vous observerez par exemple que pour 1000 tickets distribués parmi 1000 joueurs différents, la condition “intuitive” est bien vérifiée. Le “paradoxe d’Alexander” a en fait des applications en statistique théorique et en sondages.

Image de couverture © The Pokémon Company

[08] Nombre de naissances et astrologie

Un peu plus tôt dans la semaine est paru un excellent article indiquant que le pic de naissance de chaque pays dépend de sa position géographique. Aujourd’hui, on va se concentrer sur la France et visualiser la fréquence des naissances réparties par signe astrologique :

Nombre de naissances en France par signe astrologique (entre 1968 et 2005). Symboles par Par Astro_signs.svg: Tavmjongderivative work: Trex (talk) — Astro_signs.svg, CC BY 3.0, Lien — Nombre de naissances en France par signe astrologique (entre 1968 et 2005).
Symboles par Tavmjong

La différence se voit encore mieux si on se concentre sur l’écart à la moyenne :

Voilà c’est tout pour aujourd’hui ! S’il y a des passionnés d’astrologie qui veulent m’expliquer ce qu’implique ce déficit de Capricorne et cet excédent de Cancer, je prends

Données : naissances en France par jour entre 1968 et 2005.

[05] Nombre d’égalités dans les bureaux de votes

Le mois dernier, nous avions étudié la probabilité que deux candidats à une élection obtiennent le même nombre de voix étant donné leurs intentions de votes (article ici, en anglais). Peut-on appliquer la formule pour deviner le nombre de bureaux avec des égalités parfaites pour l’élection présidentielle de 2012 ?

On peut faire des hypothèses simples pour se ramener à la formule de l’article précédent : supposer que tous les bureaux ont la taille moyenne (512 électeurs par bureau), et que les intentions de vote dans chaque bureau sont les intentions de vote au niveau national c’est à dire environ 52% Hollande et 48% Sarkozy. En pratique, cette dernière hypothèse est très fausse, il suffit de regarder la carte des résultats par département pour s’en convaincre :

Avec ces hypothèses, on devrait obtenir environ 2% des bureaux avec des égalités parfaites. Attention, ce n’est qu’un ordre de grandeur (à la hausse a priori), nos hypothèses sont très simplificatrices !

Les données par bureau pour l’élection présidentielle de 2012 sont disponibles sur data.gouv. Il y a 392 bureaux avec le même nombre de voix pour Sarkozy et Hollande, soit environ 0.6% du total. Notre ordre de grandeur n’est pas si mal

[04] Collège électoral et nombre de voix du vainqueur

Il y a quelques jours, la directrice de campagne de Donald Trump s’est fait remarquer avec un tweet dans lequel elle affirmait que la victoire de Trump avec 306 voix au collège électoral était “historiquement large”. Aujourd’hui on vérifie cette affirmation en graphant le nombre de voix remportées au collège électoral pour le vainqueur de chaque présidentielle depuis 1964 (date à laquelle le collège électoral est passé à 538 voix) :

Clairement la victoire de Trump semble plutôt faire partie des marges de victoire plutôt faibles. Je croyais également me souvenir d’une victoire d’Obama assez large en 2008, mais visiblement ce n’est rien à côté des deux victoires de Reagan en 1980 et 1984 !

On peut même s’amuser à superposer le nombre de grands électeurs du vainqueur des présidentielles françaises si on supposait que la France votait comme les Etats-Unis (voir notre article de la fin du mois de novembre à ce sujet) :

A part Giscard en 1974, aucun des présidents français n’aurait gagné avec une marge inférieure à celle de Trump cette année.

[03] La date de Pâques

“Tiens, Pâques est tard l’année prochaine”. Vous avez peut-être aussi déjà entendu cette phrase à propos de Pâques 2017 ? Il est vrai que l’année prochaine, le dimanche pascal aura lieu le 16 avril, soit 20 jours plus tard qu’en 2016 (27 mars). Je me suis demandé quelle était la distribution des dates de Pâques, et quand on pouvait considérer que “Pâques tombe tôt/tard cette année”

Wikipedia nous informe que “Pâques est le dimanche qui suit le 14^e jour de la Lune qui atteint cet âge le 21 mars ou immédiatement après” … ce qui ne nous avance pas beaucoup ! Heureusement, le fameux mathématicien Gauss a établi un algorithme permettant de calculer cette fameuse date avec une suite d’opérations plutôt simples. On obtient alors la fréquence de chaque date, résumée dans ce petit graphe:

Fréquence des dates de Pâques de l'année 1600 à l'année 100000 — Fréquence des dates de Pâques de l’année 1600 à l’année 100000

Les résultats, en vrac :

Pâques ne peut avoir lieu qu’entre le 22 mars et le 25 avril
La date “moyenne” de Pâques est le 8 avril
10% des dimanches de Pâques ont lieu avant le 27 mars (donc on pouvait bien dire qu’en 2016, Pâques tombait tôt !) et 10% après le 20 avril (la prochaine fois, ce sera en 2019, le 21 avril)
La date du 19 avril est légèrement plus fréquente que les autres (prochain Pâques à cette date en 2071)
Pâques a légèrement plus de chances de tomber un jour impair qu’un jour pair (52% contre 48%)

La distribution est résumée de façon plus imagée dans ce petit calendrier :

Distribution de la date de Pâques dans le calendrier. Plus la teinte est rouge, plus la date est fréquente

A demain pour un autre petit article du calendrier de l’avent !

Riddler and Voter Power Index

Oliver Roeder has a nice puzzle: the riddler. Just like last week, this week’s puzzle has an interesting application to the US Election and I enjoyed it really much, so I figured I might just write a blog post In this article, we’ll solve this week’s riddler two different ways (just because :p) and discuss an indicator used on FiveThirtyEight’s prediction model for the election: the Voter Power Index.

Exact solution and Stirling approximation

I won’t write again the problem and notations, but you can find them here. We’ll also assume N is odd (as precised later by Ollie on Twitter). This assumption won’t matter much because we’ll only look at applications for large values of N. Let’s write:

$\mathbb{P} = \Pr(you~decide~the~election)$

Your vote is obviously going to be decisive if there is a tie between the N-1 other votes (convienently, N-1 is even). The votes are all independant with same probability p=1/2, so they are Bernoulli trials. Consequently, the probability we’re looking for is the probability that exactly half of these Bernoulli trial succeed, which is by definition the binomial distribution. Thus:

$\mathbb{P} = {{N-1}\choose{\frac{N-1}{2}}} p^{\frac{N-1}{2}} {(1-p)}^{\frac{N-1}{2}}$

As p=0.5, the exact value for the probability of your vote being decisive is thus:

$\fbox{$\mathbb{P} = \frac{{{N-1}\choose{\frac{N-1}{2}}}}{{2}^{N-1}}$}$

So, here is the exact solution, but it’s not super useful as is. Much more interesting is how this varies with N (with N sufficiently large). We can use Stirling’s approximation:

$\log \mathbb{P} = \log {{N-1}\choose{\frac{N-1}{2}}} – (N-1) \log 2 \\ ~~~~\sim N \log N – \frac{N}{2} \log \frac{N}{2} – \frac{N}{2} \log \frac{N}{2} + \frac{1}{2} \left( \log N – \log \frac{N}{2} \\~~~~~~~- \log \frac{N}{2} – \log 2\pi \right) – N \log 2 \\~~~~\sim – \frac{1}{2} \log N + \log 2 – \frac{1}{2} \log 2\pi$

Thus for sufficiently large N, the probability your vote is the decisive vote varies like the inverse of the square root of N:

$\fbox{$\mathbb{P}\sim \sqrt{\frac{2}{N\pi}} \approx \frac{0.8}{\sqrt{N}}$}$

A very simple solution for large N

Actually, we could have obtained this result for large N much more simply. We know that asymptotically the binomial distribution is gonna converge to a normal distribution. The event that your vote is the decisive one is actually the most probable event, as probabilities that the other people vote for either candidates are equal to 1/2. So the solution to the riddler can be easily computed using the density of the normal distribution:

$\mathbb{P} = \phi(0) = \frac{1}{\sqrt{2\pi \sigma^2}}$

with:

$\sigma^2 = Np(1-p) = \frac{N}{4}$

(the variance of the binomial distribution), we get the same result as in the first paragraph:

$\fbox{$\mathbb{P}\sim \sqrt{\frac{2}{N\pi}} \approx \frac{0.8}{\sqrt{N}}$}$

Mode of normal distribution for various standard deviations. © W. R. Leo

Voter Power Index

Caption from FiveThirtyEight's model — Caption from FiveThirtyEight’s model

In the US Presidential election, voters don’t elect directly their preferred candidates, but “electors” who will eventually get to vote for the president. For example, California get 55 electors while Wyoming only get 3. But divided by the number of voters in each of these states, it appears that there are approximately 510 000 voters for each elector in California while only 150 000 voters get to decide an electoral vote in Wyoming. If we assumed that probabilities of voting for each candidate was equal in these states, we can use our formula to get the relative likelihood that one vote is going to change the outcome in the election in these two states:

$\sqrt{\frac{510000}{150000}} \approx 1.8$

So in a way, a vote by a Californian is nearly 2 times less important than a vote cast in Wyoming!

Of course, probabilities are far from being equal for this year’s 2 candidates in California and Wyoming. And as Michael Vartan noted, the value of this probability matters very much!

All parameters taken into account (also including the different configurations of the electoral college in other states), this is what Nate Silver call the Voter Power Index. For this year, the probabilities that one vote will change the outcome of the whole election is highest in New Hampshire and lowest in DC.

Featured image: Number of electoral votes per voter for each state. Made using the awesome tilegram app

[Sampling] Icarus et calage sur bornes minimales au 9ème colloque francophone sondages

Du 11 au 14 octobre dernier, nous étions à Gatineau (Québec) pour participer au 9ème colloque francophone sur les sondages de la SFdS. Un grand bravo à toute l’équipe organisatrice pour ce contenu scientifique de grande qualité et ce programme social très sympathique !

Nous avons donné les présentations suivantes :

Cyril Favre-Martinoz et Thomas Merly-Alpa présentaient l’utilisation de méthodes de tirage spatialement équilibré dans le cadre de la création du nouveau plan de sondage “Nautile” de l’INSEE

Tirage spatialement équilibré – INSEE from Antoine Rebecq

Antoine Rebecq – Icarus, un package R pour le calage sur marges et ses variantes. Les slides peuvent être trouvées à l’adresse suivante : https://nc233.com/icarus
Emmanuel Gros et Antoine Rebecq – Calage sur bornes minimales et choix des bornes de calage

Calage sur bornes minimales from Antoine Rebecq
Thomas Merly-Alpa et Antoine Rebecq – Optimisation d’une allocation mixte

Optimisation d’une allocation mixte from Antoine Rebecq

Data analysis of the French football league players with R and FactoMineR

This year we’ve had a great summer for sporting events! Now autumn is back, and with it the Ligue 1 championship. Last year, we created this data analysis tutorial using R and the excellent package FactoMineR for a course at ENSAE (in French). The dataset contains the physical and technical abilities of French Ligue 1 and Ligue 2 players. The goal of the tutorial is to determine with our data analysis which position is best for Mathieu Valbuena

The dataset

A small precision that could prove useful: it is not required to have any advanced knowledge of football to understand this tutorial. Only a few notions about the positions of the players on the field are needed, and they are summed up in the following diagram:

The data come from the video game Fifa 15 (which is already 2 years old, so there may be some differences with the current Ligue 1 and Ligue 2 players!). The game features rates each players’ abilities in various aspects of the game. Originally, the grade are quantitative variables (between 0 and 100) but we transformed them into categorical variables (we will discuss why we chose to do so later on). All abilities are thus coded on 4 positions : 1. Low / 2. Average / 3. High / 4. Very High.

Loading and prepping the data

Let’s start by loading the dataset into a data.frame. The important thing to note is that FactoMineR requires factors. So for once, we’re going to let the (in)famous stringsAsFactors parameter be TRUE!

> frenchLeague <- read.csv2("french_league_2015.csv", stringsAsFactors=TRUE)
> frenchLeague <- as.data.frame(apply(frenchLeague, 2, factor))

The second line transforms the integer columns into factors also. FactoMineR uses the row.names of the dataframes on the graphs, so we’re going to set the players names as row names:

row.names(frenchLeague) <- frenchLeague$name
frenchLeague$name <- NULL

Here’s what our object looks like (we only display the first few lines here):

> head(frenchLeague)
                     foot position league age height overall
Florian Thauvin      left       RM Ligue1   1      3       4
Layvin Kurzawa       left       LB Ligue1   1      3       4
Anthony Martial     right       ST Ligue1   1      3       4
Clinton N'Jie       right       ST Ligue1   1      2       3
Marco Verratti      right       MC Ligue1   1      1       4
Alexandre Lacazette right       ST Ligue1   2      2       4

Data analysis

Our dataset contains categorical variables. The appropriate data analysis method is the Multiple Correspondance Analysis. This method is implemented in FactoMineR in the method MCA. We choose to treat the variables “position”, “league” and “age” as supplementary:

> library(FactoMineR)
> mca <- MCA(frenchLeague, quali.sup=c(2,3,4))

This produces three graphs: the projection on the factorial axes of categories and players, and the graph of the variables. Let’s just have a look at the second one of these graphs:

Projection of the players on the first two factorial axes (click to enlarge)

Before trying to go any further into the analysis, something should alert us. There clearly are two clusters of players here! Yet the data analysis techniques like MCA suppose that the scatter plot is homogeneous. We’ll have to restrict the analysis to one of the two clusters in order to continue.

On the previous graph, supplementary variables are shown in green. The only supplementary variable that appears to correspond to the cluster on the right is the goalkeeper position (“GK”). If we take a closer look to the players on this second cluster, we can easily confirm that they’re actually all goalkeeper. This absolutely makes a lot of sense: in football, the goalkeeper is a very different position, and we should expect these players to be really different from the others. From now on, we will only focus on the positions other than goalkeepers. We also remove from the analysis the abilities that are specific to goalkeepers, which are not important for other players and can only add noise to our analysis:

> frenchLeague_no_gk <- frenchLeague[frenchLeague$position!="GK",-c(31:35)]
> mca_no_gk <- MCA(frenchLeague_no_gk, quali.sup=c(2,3,4))

And now our graph features only one cluster.

Interpretation

Obviously, we have to start by reducing the analysis to a certain number of factorial axes. My favorite method to chose the number of axes is the elbow method. We plot the graph of the eigenvalues:

> barplot(mca_no_gk$eig$eigenvalue)

Around the third or fourth eigenvalue, we observe a drop of the values (which is the percentage of the variance explained par the MCA). This means that the marginal gain of retaining one more axis for our analysis is lower after the 3rd or 4th first ones. We thus choose to reduce our analysis to the first three factorial axes (we could also justify chosing 4 axes). Now let’s move on to the interpretation, starting with the first two axes:

> plot.MCA(mca_no_gk, invisible = c("ind","quali.sup"))

Projection of the abilities on the first two factorial axes

We could start the analysis by reading on the graph the name of the variables and modalities that seem most representative of the first two axes. But first we have to keep in mind that there may be some of the modalities whose coordinates are high that have a low contribution, making them less relevant for the interpretation. And second, there are a lot of variables on this graph, and reading directly from it is not that easy. For these reasons, we chose to use one of FactoMineR’s specific functions, dimdesc (we only show part of the output here):

> dimdesc(mca_no_gk)

$`Dim 1`$category
                      Estimate       p.value
finishing_1        0.700971584 1.479410e-130
volleys_1          0.732349045 8.416993e-125
long_shots_1       0.776647500 4.137268e-111
sliding_tackle_3   0.591937236 1.575750e-106
curve_1            0.740271243  1.731238e-87
[...]
finishing_4       -0.578170467  7.661923e-82
shot_power_4      -0.719591411  2.936483e-86
ball_control_4    -0.874377431 5.088935e-104
dribbling_4       -0.820552850 1.795628e-117

The most representative abilities of the first axis are, on the right side of the axis, a weak level in attacking abilities (finishing, volleys, long shots, etc.) and on the left side a very strong level in those abilities. Our interpretation is thus that axis 1 separates players according to their offensive abilities (better attacking abilities on the left side, weaker on the right side). We procede with the same analysis for axis 2 and conclude that it discriminates players according to their defensive abilities: better defenders will be found on top of the graph whereas weak defenders will be found on the bottom part of the graph.

Supplementary variables can also help confirm our interpretation, particularly the position variable:

> plot.MCA(mca_no_gk, invisible = c("ind","var"))

Projection of the supplementary variables on the first two factorial axis

And indeed we find on the left part of the graph the attacking positions (LW, ST, RW) and on the top part of the graph the defensive positions (CB, LB, RB).

If our interpretation is correct, the projection on the second bissector of the graph will be a good proxy for the overall level of the player. The best players will be found on the top left area while the weaker ones will be found on the bottom right of the graph. There are many ways to check this, for example looking at the projection of the modalities of the variable “overall”. As expected, “overall_4” is found on the top-left corner and “overall_1” on the bottom-right corner. Also, on the graph of the supplementary variables, we observe that “Ligue 1” (first division of the french league) is on the top-left area while “Ligue 2” (second division) lies on the bottom-right area.

With only these two axes interpreted there are plenty of fun things to note:

Left wingers seem to have a better overall level than right wingers (if someone has an explanation for this I’d be glad to hear it!)
Age is irrelevant to explain the level of a player, except for the younger ones who are in general weaker.
Older players tend to have more defensive roles

Let’s not forget to deal with axis 3:

> plot.MCA(mca_no_gk, invisible = c("ind","var"), axes=c(2,3))

Projection of the variables on the 2nd and 3rd factorial axes

Modalities that are most representative of the third axis are technical weaknesses: the players with the lower technical abilities (dribbling, ball control, etc.) are on the end of the axis while the players with the highest grades in these abilities tend to be found at the center of the axis:

Projection of the supplementary variables on the 2nd and 3rd factorial axes

We note with the help of the supplementary variables, that midfielders have the highest technical abilities on average, while strikers (ST) and defenders (CB, LB, RB) seem in general not to be known for their ball control skills.

Now we see why we chose to make the variables categorical instead of quantitative. If we had kept the orginal variables (quantitative) and performed a PCA on the data, the projections would have kept the orders for each variable, unlike what happens here for axis 3. And after all, isn’t it better like this? Ordering players according to their technical skills isn’t necessarily what you look for when analyzing the profiles of the players. Football is a very rich sport, and some positions don’t require Messi’s dribbling skills to be an amazing player!

Mathieu Valbuena

Now we add the data for a new comer in the French League, Mathieu Valbuena (actually Mathieu Valbuena arrived in the French League in August of 2015, but I warned you that the data was a bit old ;)). We’re going to compare Mathieu’s profile (as a supplementary individual) to the other players, using our data analysis.

> columns_valbuena <- c("right","RW","Ligue1",3,1
 ,4,4,3,4,3,4,4,4,4,4,3,4,4,3,3,1,3,2,1,3,4,3,1,1,1)
> frenchLeague_no_gk["Mathieu Valbuena",] <- columns_valbuena

> mca_valbuena <- MCA(frenchLeague_no_gk, quali.sup=c(2,3,4), ind.sup=912)
> plot.MCA(mca_valbuena, invisible = c("var","ind"), col.quali.sup = "red", col.ind.sup="darkblue")
> plot.MCA(mca_valbuena, invisible = c("var","ind"), col.quali.sup = "red", col.ind.sup="darkblue", axes=c(2,3))

Last two lines produce the graphs with Mathieu Valbuena on axes 1 and 2, then 2 and 3:

Axes 1 and 2 with Mathieu Valbuena as a supplementary individual (click to enlarge)

Axes 2 and 3 with Mathieu Valbuena as a supplementary individual (click to enlarge)

So, Mathieu Valbuena seems to have good offensive skills (left part of the graph), but he also has a good overall level (his projection on the second bissector is rather high). He also lies at the center of axis 3, which indicates he has good technical skills. We should thus not be surprised to see that the positions that suit him most (statistically speaking of course!) are midfield positions (CAM, LM, RM). With a few more lines of code, we can also find the French league players that have the most similar profiles:

> mca_valbuena_distance <- MCA(frenchLeague_no_gk[,-c(3,4)], quali.sup=c(2), ind.sup=912, ncp = 79)
> distancesValbuena <- as.data.frame(mca_valbuena_distance$ind$coord)
> distancesValbuena[912, ] <- mca_valbuena_distance$ind.sup$coord

> euclidianDistance <- function(x,y) {
 
 return( dist(rbind(x, y)) )
 
}

> distancesValbuena$distance_valbuena <- apply(distancesValbuena, 1, euclidianDistance, y=mca_valbuena_distance$ind.sup$coord)
> distancesValbuena <- distancesValbuena[order(distancesValbuena$distance_valbuena),]

> names_close_valbuena <- c("Mathieu Valbuena", row.names(distancesValbuena[2:6,]))

And we get: Ladislas Douniama, Frédéric Sammaritano, Florian Thauvin, N’Golo Kanté and Wissam Ben Yedder.

There would be so many other things to say about this data set but I think it’s time to wrap this (already very long) article up Keep in mind that this analysis should not be taken too seriously! It just aimed at giving a fun tutorial for students to discover R, FactoMineR and data analysis.