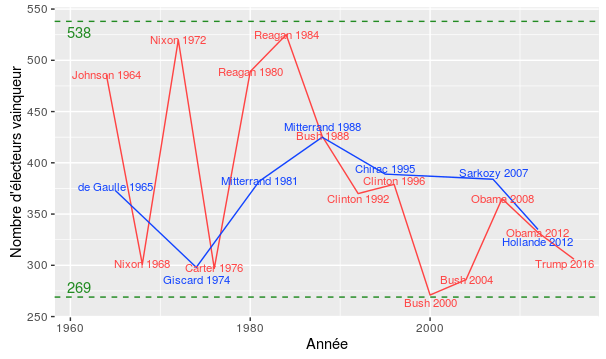
[04] Collège électoral et nombre de voix du vainqueur
Il y a quelques jours, la directrice de campagne de Donald Trump s’est fait remarquer avec un tweet dans lequel elle affirmait que la victoire de Trump avec 306 voix au collège électoral était “historiquement large”. Aujourd’hui on vérifie cette affirmation en graphant le nombre de voix remportées au collège électoral pour le vainqueur de chaque présidentielle depuis 1964 (date à laquelle le collège électoral est passé à 538 voix) : Clairement la victoire de Trump semble plutôt faire partie des…