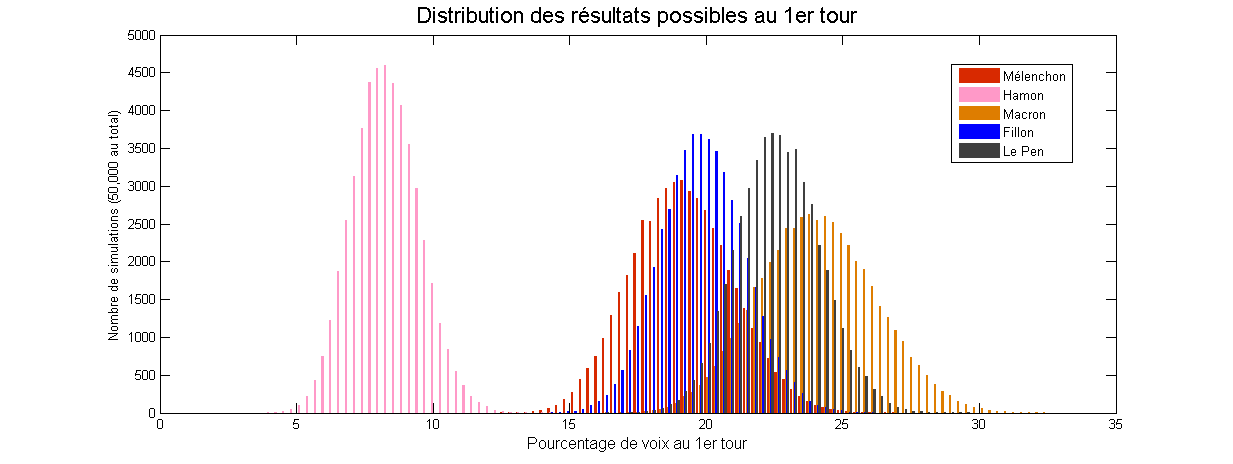
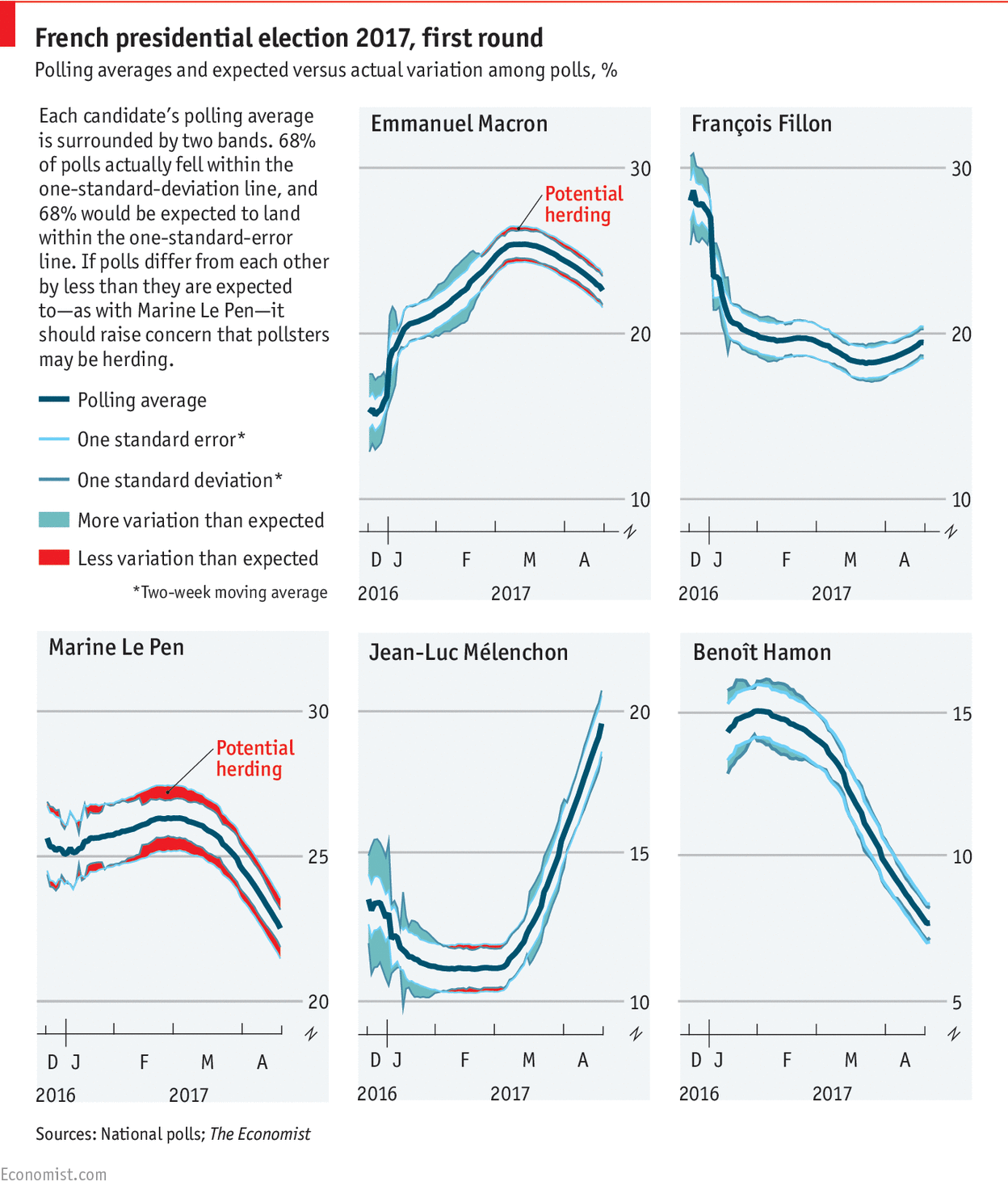
Graph sampling for machine learning at Montreal AI Symposium
I’ll be at the 2019 Montreal AI Symposium today, presenting a poster about Network sampling and an application to Machine Learning: Network sampling and applications to big data and machine learning from Antoine Rebecq Featured image: Montreal Skyline, by Taxiarchos228