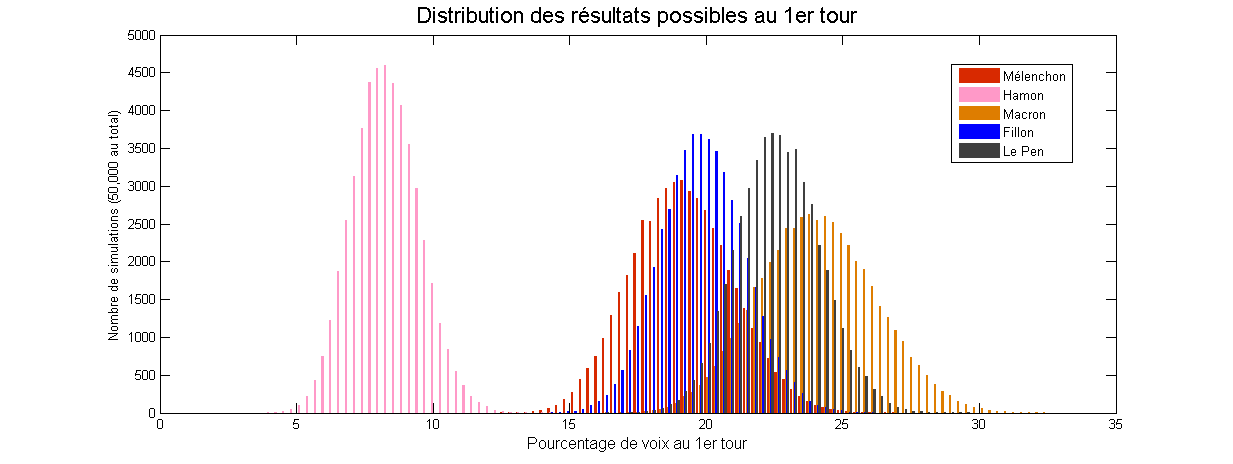
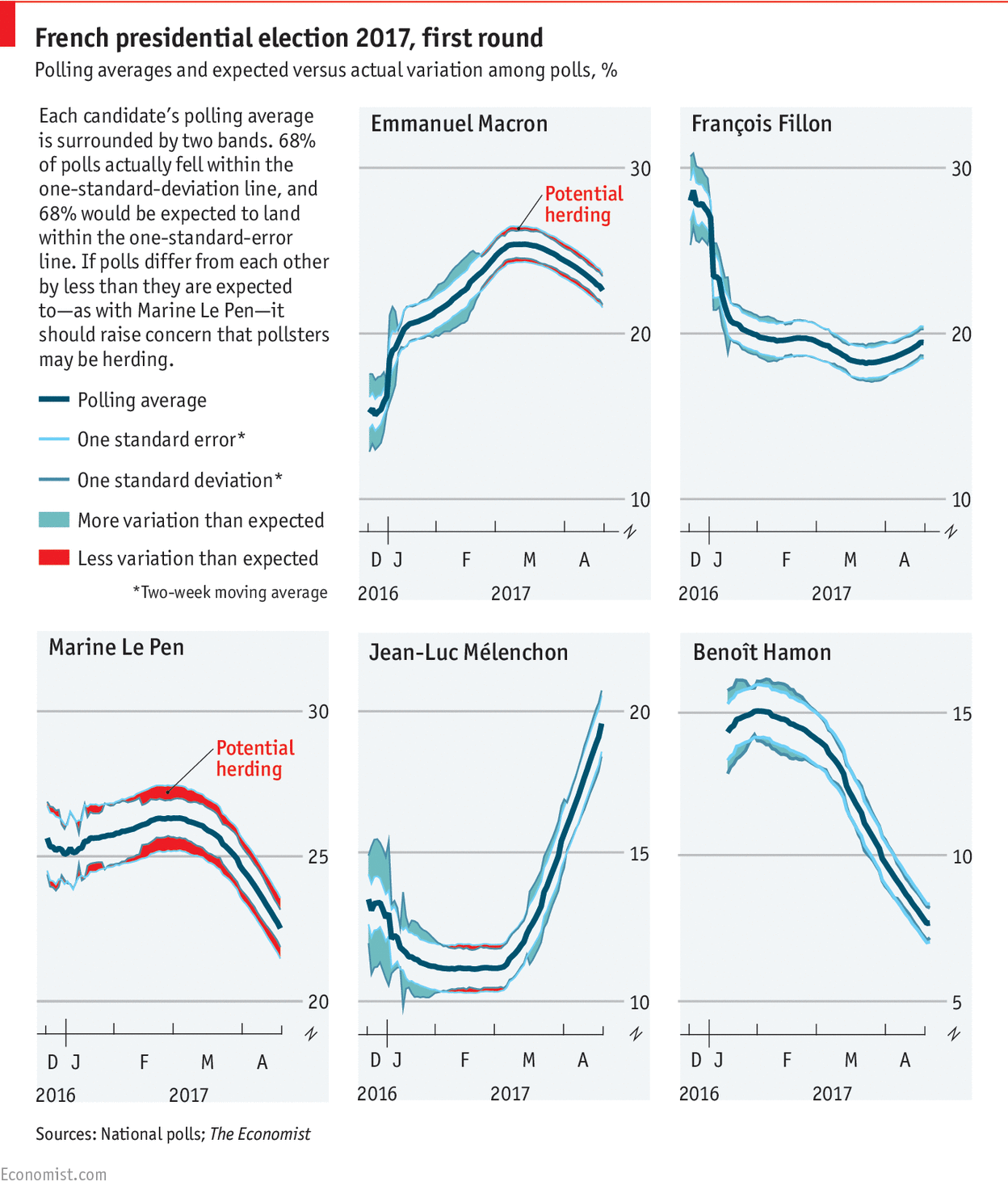
Marges d’erreurs, approche modèle et sondages
Si cette élection présidentielle aura permis quelque chose, c’est bien d’avoir des discussions intéressantes sur les sondages ! Cette course à quatre est inédite dans l’histoire de la Vème République, et avec les grosses surprises de l’actualité récente (Trump et Brexit), il est normal de s’interroger sur l’incertitude réelle contenue dans ces données de sondages. Je propose donc de parler aujourd’hui des “marges d’erreurs” (dits aussi “intervalles de confiance à 95%”) qui ont pour but de quantifier cette incertitude. Je…