Les sondages peuvent parfois faire l’actualité sans parler de politique ! Prenons l’exemple de l’affaire qui oppose Fun Radio et l’institut Médiamétrie, qui est chargé de la mesure d’audience sur les chaînes de télé, de radio, et même des sites internet. Un animateur de la matinale de la radio avait demandé à ses auditeurs, dans le cas où ils seraient contactés par Médiamétrie, de déclarer qu’ils n’écoutaient que Fun Radio (et aucune radio), et qu’ils étaient à l’écoute de la station durant toute la journée. Cela a conduit Médiamétrie à retirer momentanément Fun Radio du panel de mesure. Cette décision a eu des conséquences importantes sur les finances de la radio : en effet, la répartition des revenus publicitaires est directement indexée sur ces calculs d’audience. Ainsi, la radio s’est pourvu en justice pour être réintégrée, ce qui sera a priori le cas.
Je ne commenterai pas la décision de justice, n’y connaissant rien, mais j’ai plutôt envie de commenter d’un point de vue de sondeur cette affaire. En effet, si l’on résume, les messages ont eu (potentiellement) trois effets :
- Encourager les auditeurs de la matinale à répondre aux enquêteurs de Médiamétrie lorsque ceux-ci les contactent ;
- Sur-déclarer un temps d’écoute pour la radio Fun Radio ;
- Sous-déclarer un temps d’écoute pour d’autres radios.
À mon sens, ces trois problèmes demandent des solutions différentes ! Je vais laisser le premier de coté, qui me semble le plus intéressant d’un point de vue sondages, pour parler brièvement des deux autres.
Tout d’abord le deuxième : on peut imaginer qu’en utilisant des sources extérieures comme le panel Radio global sur le temps d’écoute moyen de la radio en France, ou des enquêtes type Emploi du Temps de l’INSEE, on puisse repérer des outliers (c’est à dire des personnes qui déclarent des valeurs qui sortent très largement de la moyenne) et les traiter, ou les exclure. En gros, écouter la radio 24h par jour, c’est suspect.
Le troisième point est le plus ardu à corriger, mais on peut faire l’hypothèse (soyons optimistes) que quelqu’un qui est prêt à mentir si un animateur radio le lui demande est un auditeur exclusif de la radio en question, ce qui neutralise l’effet.
Reste donc le premier point. Tout praticien des sondages sait que les individus sélectionnés dans un échantillon ne sont pas tous volontaires pour répondre aux questionnaires, loin de là. Cela crée un biais, qui est étudié et traité en statistiques par des méthodes de “correction de la non-réponse”. On pourrait donc imaginer que ces méthodes servant à prendre en compte la non-réponse pourraient suffire à annuler le biais en question, mais le problème est plus compliqué que cela. Je vais tenter d’expliquer à l’aide d’un exemple : supposons qu’il existe uniquement deux radios, une pour les “jeunes”, et une pour les autres. Dans ce cas, Médiamétrie cherche à savoir combien de personnes écoutent chaque radio. Si 10% des jeunes répondent avant l’effet de l’annonce, Médiamétrie a l’habitude de multiplier par 10 (pour simplifier) le nombre d’auditeurs de Fun Radio : si le nombre de répondants augmente, il suffit de changer un peu le coefficient multiplicatif, mais cela n’aura pas d’effet sur l’écoute de l’autre radio, et les chiffres devraient être globalement les mêmes.
Pourquoi je dis que c’est plus compliqué ? Parce que les méthodes de la correction de la non-réponse reposent sur de l’information auxiliaire, par exemple les informations démographiques. On peut facilement séparer (par exemple via les variables d’âge) l’auditeur moyen de Fun Radio de celui de France Inter, mais ce sera plus compliqué avec NRJ ou une autre station destinée à un même public. Il est d’ailleurs intéressant de noter que c’est NRJ qui a initialement porté réclamation auprès de Médiamétrie. Et donc, la mesure “absolue” de l’audience de Fun Radio (en excluant les points 2 et 3) n’est pas trop mauvaise. Celle de Nostalgie n’est pas impactée non plus, mais celle de NRJ peut l’être énormément. En effet, plus de jeunes répondent, mais les répondants écoutent moins NRJ (car ils sont plutôt auditeurs de Fun Radio), donc l’estimation finale est à la baisse pour cette radio, alors que le comportement de leurs auditeurs n’a pas changé.
Voilà, vous en savez plus sur ceux qui travaillent en secret pour Médiamétrie !

![[22] L’affaire “Fun Radio”](https://nc233.com/wp-content/uploads/2016/12/2048x1536-fit_illustration-fun-radio-825x510.jpg)
![[21] Lettres internationales](https://nc233.com/wp-content/uploads/2016/12/1958_US_Airmail_Stamped_Envelope_Indicium_-_7cents-825x510.jpg)
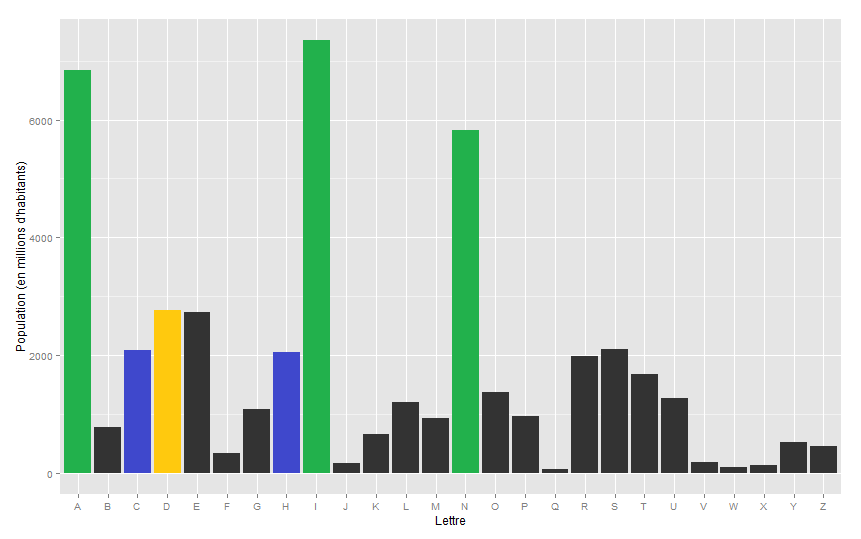
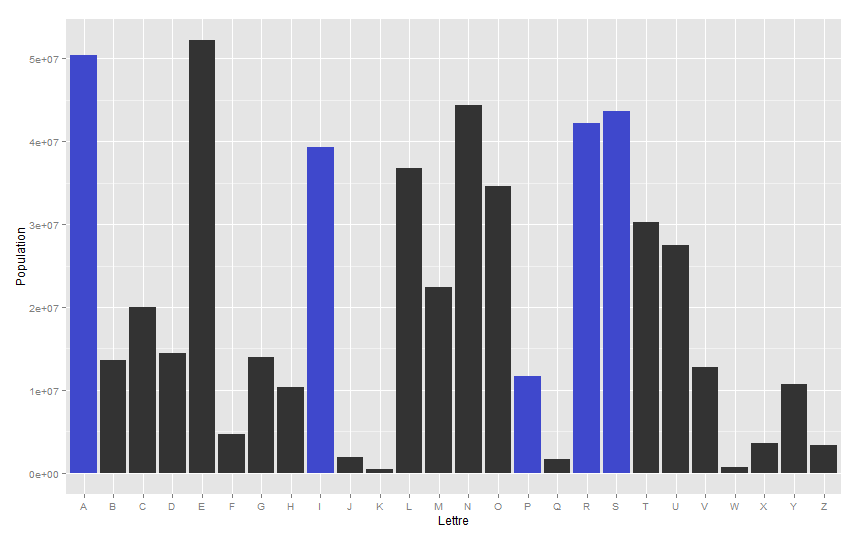
![[17] Avenue, Rue ou Boulevard Jean Jaurès ?](https://nc233.com/wp-content/uploads/2016/12/dscf3643-825x510.jpg)
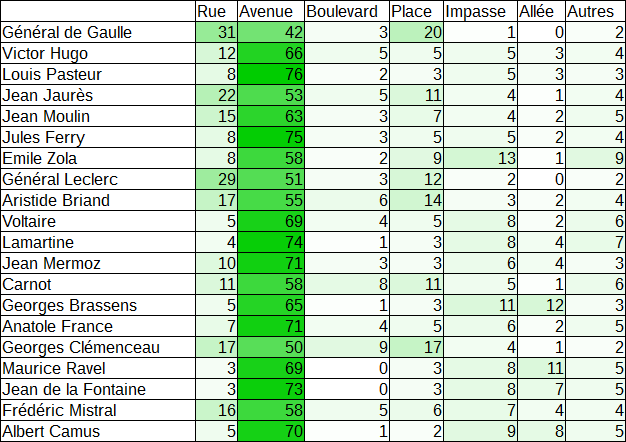
![[16] Lettres de France](https://nc233.com/wp-content/uploads/2016/12/Musee_de_la_poste_Boites_aux_lettres_anciennes-825x510.jpg)
![[15] Fuseaux horaires européens](https://nc233.com/wp-content/uploads/2016/12/business-time-clock-clocks-48770-825x510.jpeg)
![[14] Noms de rues et personnalités](https://nc233.com/wp-content/uploads/2016/12/Paris_13e_-_boulevard_du_Général-de-Gaulle_1-825x510.jpg)
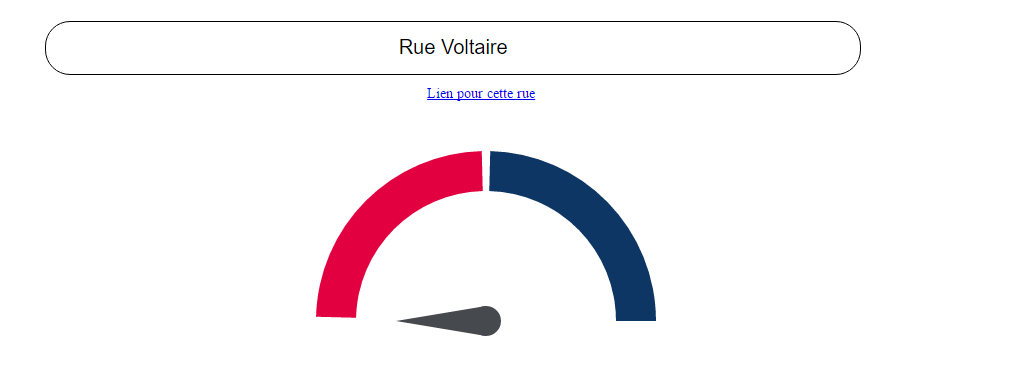
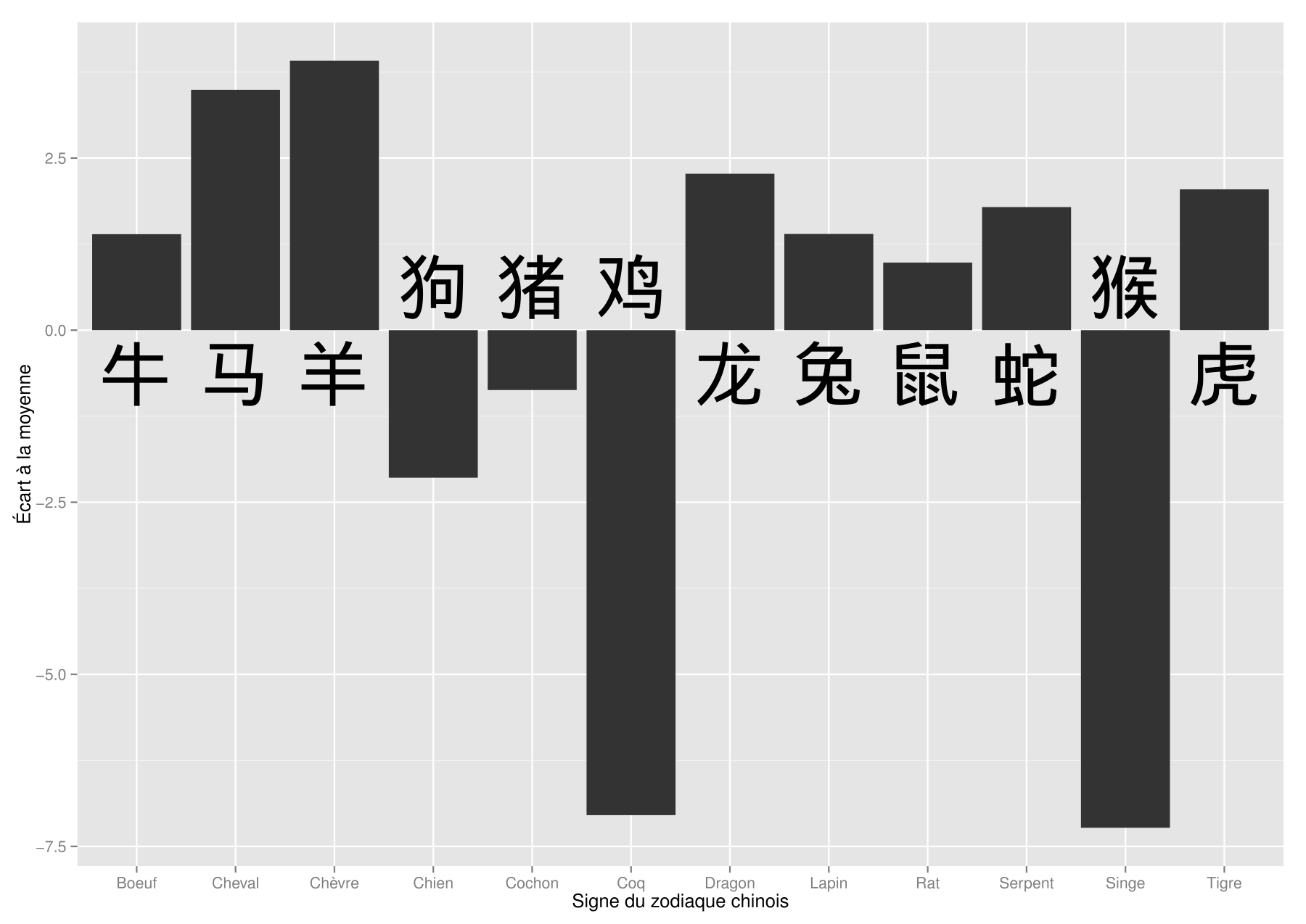
![[11] Nombre de naissances et astrologie chinoise](https://nc233.com/wp-content/uploads/2016/12/Les_douze_animaux_2-825x335.jpg)
![[10] Big data et statistique publique](https://nc233.com/wp-content/uploads/2016/12/graphe1-825x510.png)
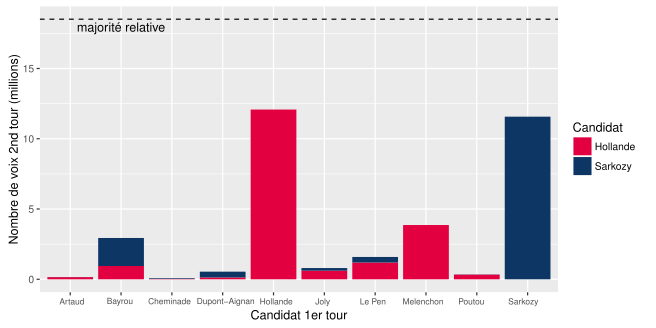
![[09] Reports de voix à la présidentielle 2012](https://nc233.com/wp-content/uploads/2016/12/plot_report_relatif.png)
![[07] Nombre d’occupants par pièce en France](https://nc233.com/wp-content/uploads/2016/12/Logement-825x510.jpg)
