Category: Uncategorized

(Ce petit article est une reprise d’un fil twitter fait à l’occasion du Final Four de la NCAA)

Aujourd’hui on propose de prendre un peu de temps pour discuter des notions de “chance” (luck) et de “talent” (skill) dans le domaine du sport, en s’inspirant d’arguments exposés dans The Success Equation: Untangling Skill and Luck in Business, Sports, and Investing, sorti en 2012. La question qui se pose est la suivante : dans les résultats d’une équipe sportive ou d’un athlète, qu’est-ce qui vient de l’habileté et qu’est-ce qui relève uniquement de la chance ? Même si l’on faisait l’hypothèse que le déterminant principal d’un résultat est le talent de l’athlète, certaines sous-performances peuvent arriver.

C’est un sujet assez classique, qui est développé dans la plupart des études statistiques sur le sport. Pour ceux qui préfèrent le format vidéo, voici un résumé rapide de ce qu’explique le livre :

Mathématiquement, on considère que le skill et la chance sont deux variables indépendantes. On peut donc écrire une équation très simple sur leur variance :

Var(observations) = Var(skill) + Var(chance)

Cela nous donne donc une façon d’estimer la contribution du skill dans les résultats, c’est à dire une idée de l’importance du talent de l’athlète :

Var(skill) = Var(observations) – Var(chance)

Plus ce terme est important, plus les résultats obtenus proviennent du fait que le sport récompense les joueurs qui ont du talent. Dans un jeu complètement aléatoire (pile ou face…), c’est uniquement la chance qui amène au résultat final. On imagine alors que chaque sport va plus ou moins s’éloigner de ce modèle.

Nous avions discuté de cette question par rapport au badminton et au tennis ; on constatait alors que, grâce à la règle de l’écart des deux points, il y avait une plus grande stabilité des victoires (et donc une plus faible part de chance) au tennis qu’au badminton. Une même question se posait sur le tir à l’arc, avec le changement des règles qui permet plus facilement de rattraper une flèche ratée.

Comment faire pour estimer cette contribution ? Pour le premier terme, Var(observations), c’est facile. On considère les résultats (d’une saison par exemple) comme une variable aléatoire et on calcule sa variance. On constate que certains sports sont plus variables que d’autres, par exemple le basket par rapport au hockey :

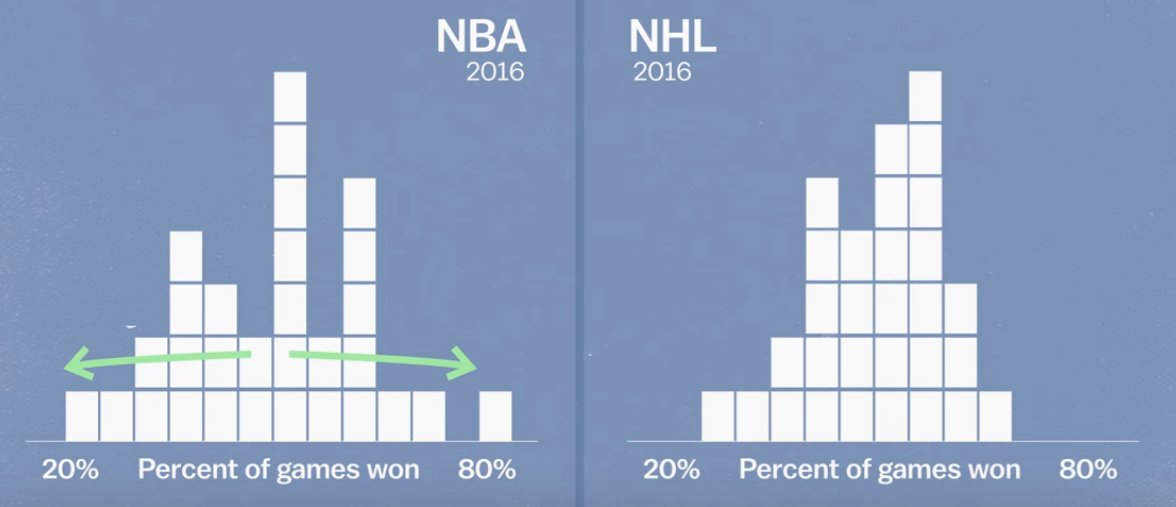
Le seconde terme, Var(chance), est un peu plus complexe à estimer. Dans son son livre, Mauboussin prend chaque match comme une expérience de Bernoulli (avec une probabilité de victoire qui correspond au taux de victoire dans la saison). Il obtient donc, par sport, un pourcentage d’explication du skill dans le résultat final. Par exemple, pour la NBA il obtient 88% et pour la NHL 47%.

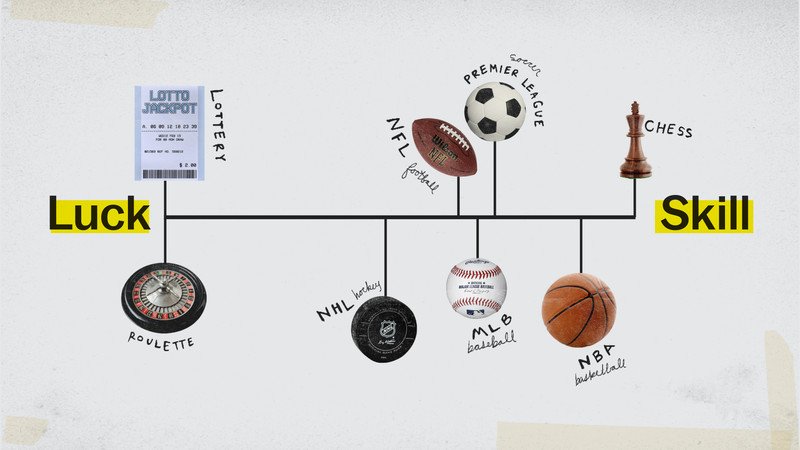
Une bonne part de la variance s’explique en fait par le nombre de matches joués, qui correspond dans la logique à la “taille d’échantillon”. La NFL (16 matches / saison) est donc logiquement plus aléatoire que la NBA (82 matches / saison) sur l’axe skill / chance représenté en haut de l’article. On peut aussi appliquer le même concept en considérant chaque “action” comme une expérience aléatoire. Par exemple, chaque possession au basket, comme une chance de marquer avec une certaine probabilité. C’est pour cela l’on s’attendait à ce que l’underdog Loyola-Chicago essaye de jouer le plus lentement possible.

L’idée derrière cette stratégie est que moins de possessions implique plus de variance et donc moins de chances de l’emporter pour le favori ; en effet, plus l’on joue, plus l’aléatoire doit s’équilibrer et donc le talent va s’imposer. La validité de cette stratégie est disputée : certaines analyses statistiques ont montré que les chances de victoires des équipes mal classées (underdogs) contre des équipes réputées bien meilleures n’était pas modifiées par le rythme du match.

Pour conclure, le même genre d’analyse a été appliqué récemment (avec plus ou moins de succès) à l’esport. Yauheni Hladki a présenté à la GDC une analyse dont le résultat situe tous les jeux (oui, tous, même Hearthstone) à la droite des échecs sur l’axe skill / chance. Ce qui signifierait que la chance aurait moins d’impact sur le résultat que dans la plupart des sports. En d’autres termes, qu’une équipe mal classée de CS:GO n’aurait que des chances infimes de remporter un match contre une équipe du top mondial… pas terrible pour le suspense si cela était vrai !

La “clé” derrière ce résultat est que l’auteur considère chaque action effectuée en esport comme une expérience aléatoire. Cela inclut par exemple chacun des tirs effectués dans une partie de CS:GO ! La taille d’échantillon “équivalent” considérée est énorme (la variance obtenue est donc très faible) et c’est ce qui le conduit à placer tous les esports au même endroit sur l’axe. À vous de juger de la pertinence de cette méthode !

 

Last week we published the results of our prediction model for UEFA Euro 2016. Here are a few comments.

This Euro is undecided

Our model gives fairly close probabilities of winning. To us, this suggests that the competition is fairly open and that no team is a clear favorite before the competition starts (we really hope to see that change after a few matches!)

One could object that this merely shows that our model is unable to predict an outcome with adequate confidence, so we ran the simulations after injecting an artificially low variance in our model, and results for the top teams turned out to be very similar: no clear favorite emerged.

Historically, the European Championship has always been somewhat undecided. Whereas only 8 different teams ever became World Champions (20 editions of the World Cup were held), 9 different teams have already won a European Championship in just 14 editions! In some cases, complete underdogs eventually won the title (for example Denmark in 1992 or Greece in 2004).

France is one of the favorites

The home team is every other’s model favorite! Check out Goldman Sachs’ or a model built by Austrian researchers based on bookmakers’ odds. Clearly, the home advantage is key here, although recently France has proven able to score quite a number of goals, which is an important feature of our model. The model’s favorite is Belgium (who are, the start of the competition, 2nd in the Fifa rankings), but Germany, Spain and England are very close.

Interestingly, even if our model selects France as one of its favorite, it predicts that the group phase won’t be as easy as it seems. For example, the most likely scenario for the opening match is a draw. The probability of reaching the second round is high (86%), but it’s only the fifth highest of values (which might be surprising if you consider that France’s first round opponents are really far behind in the Fifa/Elo rankings). This is very different from other models and bookies, who make France a very heavy favorite to end up at the first place of the group.

As a supporter of France, this reminds us a few (good) memories. In 2000, France only finished second of its group to the Netherlands (and still won the competition), while in the 2006 World Cup, France barely qualified among relatively weak teams, and still managed to reach the final.

Zlatan may not be enough

Altough Sweden, partly thanks to its legendary striker Zlatan Ibrahimovic, is generally said to be a fairly good team, it has the lowest probability of reaching the round of 16 (24.1%), slightly behind Iceland and Albania. In fact, Sweden was very unlucky during the draw and ended up in the so-called “group of death” along with two top tier teams (Belgium and Italy), and an outsider (Ireland) that our model predicts not so bad.

Are Switzerland and Hungary undervalued?

The biggest difference between our model and the bookies’ odds (or the other models) is the relatively high probability we put on Switzerland’s win (6% for us, 1% for Goldman Sachs for instance). It’s hard to really say why our model predicts they’ll fare so well, but we’re definitely impatient to see if this checks out 🙂

Our model also says Hungary is generally under-estimated: to it, the heirs of the “Magikus Magyarok” might very well fight for second place in Group F, while in most predictions they finish dead last.

EDIT: a previous version of this article presented France as the model’s favorite, which was the consequence of a bug that occurred for the second-round probabilities. It is now corrected. Other conclusions are unchanged.