NC233

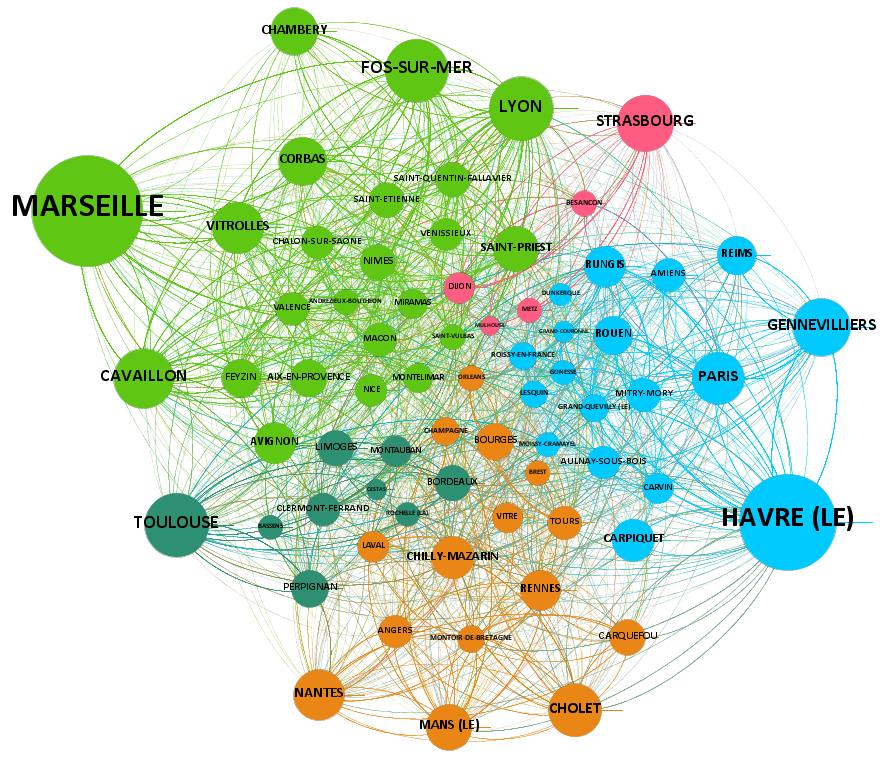
Le 30 novembre dernier a eu lieu le dernier séminaire de méthodologie statistique (SMS) de l’INSEE. Il portait sur le Big Data et la statistique publique, en mettant l’accès sur les méthodes utilisées : logiciels spécifiques, machine learning, étude des réseaux, étude textuelle… Les résumés des présentations sont disponibles ici. Cela a été l’occasion de diffuser le blog statoscope (très bon jeu de mot). Il possède plusieurs articles expliquant certaines techniques utilisées dans le cadre du traitement de données massives,…

Read More Read More

La question du report des voix entre les deux tours des élections est souvent primordiale pour les politologues et les journalistes politiques, afin de mieux comprendre les rapports de force entre les candidats. En effet, les candidats non qualifiés donnent ou non des consignes de vote, ou ont des proximités politiques plus ou moins claires avec un des candidats qualifiés pour le second tour. Nous allons essayer d’aborder cette question en regardant les deux tours de l’élection présidentielle française de…

Read More Read More

Un peu plus tôt dans la semaine est paru un excellent article indiquant que le pic de naissance de chaque pays dépend de sa position géographique. Aujourd’hui, on va se concentrer sur la France et visualiser la fréquence des naissances réparties par signe astrologique : La différence se voit encore mieux si on se concentre sur l’écart à la moyenne : Voilà c’est tout pour aujourd’hui ! S’il y a des passionnés d’astrologie qui veulent m’expliquer ce qu’implique ce déficit de…

Read More Read More

Les données INSEE issues du recensement de la population, qui a lieu tous les ans (enfin, on ne peut pas être recensé tous les ans, car il s’agit d’un cycle sur cinq ans) permettent de récupérer beaucoup d’informations “basiques” sur les populations et les logements. Nous allons nous intéresser ici à une question : combien de personnes vivent en moyenne dans une pièce d’un logement ? C’est à dire que l’on calcule pour chaque commune française le nombre total de…

Read More Read More

Aujourd’hui, c’est homicide ! Je suis tombé sur une datavisualisation de StatCanada sur les homicides au Canada. Si ça vous intéresse, cliquez sur l’image ci-dessous : En France, ces données sont centralisées par l’Observatoire national de la délinquance et des réponses pénales (ONDRP), qui publie ses données sur data.gouv. Leur dernier rapport est disponible ici.

Le mois dernier, nous avions étudié la probabilité que deux candidats à une élection obtiennent le même nombre de voix étant donné leurs intentions de votes (article ici, en anglais). Peut-on appliquer la formule pour deviner le nombre de bureaux avec des égalités parfaites pour l’élection présidentielle de 2012 ? On peut faire des hypothèses simples pour se ramener à la formule de l’article précédent : supposer que tous les bureaux ont la taille moyenne (512 électeurs par bureau), et…

Read More Read More

Il y a quelques jours, la directrice de campagne de Donald Trump s’est fait remarquer avec un tweet dans lequel elle affirmait que la victoire de Trump avec 306 voix au collège électoral était “historiquement large”. Aujourd’hui on vérifie cette affirmation en graphant le nombre de voix remportées au collège électoral pour le vainqueur de chaque présidentielle depuis 1964 (date à laquelle le collège électoral est passé à 538 voix) : Clairement la victoire de Trump semble plutôt faire partie des…

Read More Read More

Nous avons décidé de réaliser notre propre calendrier de l’avent ! Aujourd’hui, nous reparlons de l’élection américaine. Aux détours des Internets, je suis tombé sur un article de blog qui suivait un peu la même idée que celle que nous avions développé dans notre dernier article long : comment adapter le système de vote américain, avec ses états et ses grands électeurs, à un autre pays ou à une autre zone géographique ? Son idée est d’utiliser les votes des…

Read More Read More

Nous avons décidé de réaliser notre propre calendrier de l’avent ! Tous les jours, vous trouverez un petit article ou une reprise d’un jeu de données, d’une publication ou d’un post d’un autre blog que nous avons trouvé particulièrement intéressant. Aujourd’hui, nous allons parler de sondages, et en particulier de sondages pour instituts en manque de moyens. Supposons que l’on réalise un vote auprès d’un grand nombre d’électeurs, disons un million. Notre institut de sondages, l’IPFRES, souhaiterait savoir lequel des…

Read More Read More