I’ll be at the 2019 Montreal AI Symposium today, presenting a poster about Network sampling and an application to Machine Learning:
Featured image: Montreal Skyline, by Taxiarchos228
I’ll be at the 2019 Montreal AI Symposium today, presenting a poster about Network sampling and an application to Machine Learning:
Featured image: Montreal Skyline, by Taxiarchos228
Demain (jeudi 8 novembre), je donnerai une présentation au Symposium de méthodologie de Statistiques Canada sur la mise en place du nouveau système d’échantillonnage de l’INSEE pour les enquêtes auprès des ménages et des individus à partir des sources fiscales.
Ce changement de base apporte de nouvelles opportunités (nouvelles variables, nouveaux moyens de contact, meilleure coordination des enquêtes) mais aussi des défis (concordance des concepts, gestion du champ de la base administrative).
Les acétates sont ci-dessous :
Tomorrow (November 7th), I’ll give a talk at the Statistics Canada Symposium on survey sampling and big data.
I’ll show how techniques that were developed at official statistics institutes can now be used in the context of big data and machine learning, and add a lot of value. I’ll show some examples with:
And really glad to be returning to Ottawa, even though the trip will be short!
Featured image: Parliament Hill, by Taxiarchos228
Calibration in survey sampling is a wonderful tool, and today I want to show you how we can use it in some Machine Learning applications, using the R package Icarus. And because ’tis the season, what better than a soccer dataset to illustrate this? The data and code are located on this gitlab repo: https://gitlab.com/haroine/weighting-ml

First, let’s start by installing and loading icarus and nnet, the two packages needed in this tutorial, from CRAN (if necessary):
install.packages(c("icarus","nnet"))
library(icarus)
library(nnet)
Then load the data:
load("data/weighting_ML_part1.RData")
The RData file contains two dataframes, one for the training set and one for the test set. They contain results of some international soccer games, from 01/2008 to 12/2016 for the training set, and from 01/2017 to 11/2017 for the test. Along with the team names and goals scored for each side, a few descriptive variables that we’re going to use as features of our ML models:
> head(train_soccer) Date team opponent_team home_field elo_team 1 2010-10-12 Belarus Albania 1 554 2 2010-10-08 Bosnia and Herzegovina Albania 0 544 3 2011-06-07 Bosnia and Herzegovina Albania 0 594 4 2011-06-20 Argentina Albania 1 1267 5 2011-08-10 Montenegro Albania 0 915 6 2011-09-02 France Albania 0 918 opponent_elo importance goals_for goals_against outcome year 1 502 1 2 0 WIN 2010 2 502 1 1 1 DRAW 2010 3 564 1 2 0 WIN 2011 4 564 1 4 0 WIN 2011 5 524 1 2 3 LOSS 2011 6 546 1 2 1 WIN 2011
elo_team and opponent_elo are quantitative variables indicative of the level of the team at the date of the game ; importance is a measure of high-profile the game played was (a friendly match rates 1 while a World Cup game rates 4). The other variables are imo self-descriptive.
Then we can train a multinomial logistic regression, with outcome being the predicted variable, and compute the predictions from the model:
outcome_model_unw <- multinom(outcome ~ elo_team + opponent_elo + home_field + importance, data = train_soccer) test_soccer$pred_outcome_unw <- predict(outcome_model_unw, newdata = test_soccer)
The sheer accuracy of this predictor is kinda good:
> ## Accuracy > sum(test_soccer$pred_outcome_unw == test_soccer$outcome) / nrow(test_soccer) [1] 0.5526316
but it has a problem: it never predicts draws!
> summary(test_soccer$pred_outcome_unw) DRAW LOSS WIN 0 208 210
And indeed, draws being less common than other results, it seems more profitable for the algorithm that optimizes accuracy never to predict them. As a consequence, the probabilities of the game being a draw is always lesser than the probability of one team winning it. We could show that the probabilities are not well calibrated.
A common solution to this problem is to use reweighting to correct the imbalances in the sample, which we’ll now tackle. It is important to note that the weighting trick has to happen in the training set to avoid “data leaks”. A very good piece on this subject has been written by Max Kuhn in the documentation of caret.

Commonly, you would do:
train_soccer$weight <- 1 train_soccer[train_soccer$outcome == "DRAW",]$weight <- (nrow(train_soccer)/table(train_soccer$outcome)[1]) * 1/3 train_soccer[train_soccer$outcome == "LOSS",]$weight <- (nrow(train_soccer)/table(train_soccer$outcome)[2]) * 1/3 train_soccer[train_soccer$outcome == "WIN",]$weight <- (nrow(train_soccer)/table(train_soccer$outcome)[3]) * 1/3
> table(train_soccer$weight) 0.916067146282974 1.22435897435897 3336 1248
The draws are reweighted with a factor greater than 1 and the other games with a factor lesser than 1. This balances the predicted outcomes and thus improves the quality of the probabilities …
outcome_model <- multinom(outcome ~ elo_team + opponent_elo + home_field + importance,
data = train_soccer,
weights = train_soccer$weight)
test_soccer$pred_outcome <- predict(outcome_model, newdata = test_soccer)
> summary(test_soccer$pred_outcome) DRAW LOSS WIN 96 167 155
… though at a loss in accuracy:
> ## Accuracy > sum(test_soccer$pred_outcome == test_soccer$outcome) / nrow(test_soccer) [1] 0.5263158
Now let’s look at the balance of our training sample on other variables:
> round(table(test_soccer$importance) / nrow(test_soccer),2) 1 2 3 4 0.26 0.08 0.54 0.12 > round(table(train_soccer$importance) / nrow(train_soccer),2) 1 2 3 4 0.56 0.08 0.23 0.12
It seems that the test set features a lot more important matches than the training set. Let’s look further, in particular at the dates the matches of the training set were played:
> round(table(train_soccer$year) / nrow(train_soccer),2) 2008 2009 2010 2011 2012 2013 2014 2015 2016 0.10 0.11 0.11 0.10 0.11 0.13 0.11 0.11 0.12
Thus the matches of each year between 2008 and 2016 have the same influence on the final predictor. A better idea would be to give the most recent games a slightly higher influence, for example by increasing their weight and thus reducing the weights of the older games:
nyears <- length(unique(train_soccer$year)) year_tweak <- rep(1/nyears,nyears) * 1:nyears year_tweak <- year_tweak * 1/sum(year_tweak) ## Normalization
> year_tweak [1] 0.02222222 0.04444444 0.06666667 0.08888889 0.11111111 0.13333333 [7] 0.15555556 0.17777778 0.20000000
We determine it is thus a good idea to balance on these two additional variables (year and importance). Now how should we do this? A solution could be to create an indicator variable containing all the values of the cross product between the variables outcome, year and importance, and use the same reweighting technique as before. But this would not be very practical and more importantly, some of the sub-categories would be nearly empty, making the procedure not very robust. A better solution is to use survey sampling calibration and Icarus 🙂
train_soccer$weight_cal <- 1
importance_pct_test <- unname(
table(test_soccer$importance) / nrow(test_soccer),
)
marginMatrix <- matrix(, nrow = 0, ncol = 1) %>% ## Will be replaced by newMarginMatrix() in icarus 0.3.2
addMargin("outcome", c(0.333,0.333,0.333)) %>%
addMargin("importance", importance_pct_test) %>%
addMargin("year", year_tweak)
train_soccer$weight_cal <- calibration(data=train_soccer, marginMatrix=marginMatrix,
colWeights="weight_cal", pct=TRUE, description=TRUE,
popTotal = nrow(train_soccer), method="raking")
outcome_model_cal <- multinom(outcome ~ elo_team + opponent_elo + home_field + importance,
data = train_soccer,
weights = train_soccer$weight_cal)
test_soccer$pred_outcome_cal <- predict(outcome_model_cal, newdata = test_soccer)
icarus gives a summary of the calibration procedure in the log (too long to reproduce here). We then observe a slight improvement in accuracy compared to the previous reweighting technique:
> sum(test_soccer$pred_outcome_cal == test_soccer$outcome) / nrow(test_soccer) [1] 0.5478469
But more importantly we have reason to believe that the we improved the quality of the probabilities assigned to each event (we could check this using metrics such as the Brier score or calibration plots) 🙂
It is also worth noting that some algorithms (especially those who rely on bagging, boosting, or more generally on ensemble methods) naturally do a good job at balancing samples. You could for example rerun the whole code and replace the logit regressions by boosted algorithms. You would then observe fewer differences between the unweighted algorithm and its weighted counterparts.
Stay tuned for the part 2, where we’ll show a trick to craft better probabilities (particularly for simulations) using external knowledge on probabilities.
Il y a une semaine quasiment jour pour jour, dimanche 23 avril à 20h, les résultats du premier tour de l’élection présidentielle ont été annoncés sur les plateaux des grandes chaînes, TF1 ou France Télévisions par exemple. Pour donner ce résultat, il n’est pas envisageable d’attendre les remontées officielles, qui n’arrivent que tard dans la nuit, une fois que tous les bureaux ont été dépouillés. D’autre part, il ne serait pas très pertinent de récupérer les résultats au fur et à mesure des remontées des bureaux dépouillés, car on sait que les premiers sont souvent ceux des communes rurales, qui ne votent pas du tout comme les autres. Il est donc nécessaire de procéder par estimations. Pour cela, les grands instituts de sondage partenaires des soirées électorales de chacune des chaînes sélectionnent certains bureaux de vote et remontent l’information sur les premiers bulletins dépouillés : cela suffit à obtenir une précision suffisante, couplée à certains modèles de prédiction sur les caractéristiques des bureaux (à ce sujet, difficile d’être plus précis, les instituts gardant jalousement leurs méthodes secrètes !).
Nous allons ici nous intéresser à un moyen de bien sélectionner les bureaux de vote dans lequel faire remonter l’information, en utilisant ce que l’on appelle le sondage équilibré. Le sondage équilibré (voir par exemple ici, attention technique) revient à choisir au hasard un échantillon qui respecte certaines conditions de structure (ce qu’on pourrait appeler, de façon abusive, un échantillon représentatif). Par exemple, lorsque l’on échantillonne des individus, on peut souhaiter avoir le bon nombre d’hommes et de vieux, de jeunes et de plus âgés, etc. Attention ! On ne parle pas ici de méthode de quotas, mais bien d’un sondage aléatoire où on tire certains individus au hasard parmi une population connue mais en faisant en sorte de respecter la structure voulue. Les méthodes de sondage équilibré sont assez complexes, mais elles sont très étudiées en sondage.
Ici, la population, ce sont les bureaux de vote pour l’élection présidentielle 2017 (données ici). Nous allons essayer d’équilibrer notre échantillon sur les votes à l’élection présidentielle de 2012, c’est à dire les choisir de telle sorte que si on avait choisi ces bureaux en 2012, on aurait eu le bon score (ou quasiment le bon score) pour les principaux candidats. L’idée est que le vote en 2017 et celui en 2012 sont assez liés : c’est d’ailleurs une des raisons qui fait que les sondages français sont précis mais souvent proches les uns des autres. Nous allons donc sélectionner 100 bureaux de vote (sur les 70 000 environ) de cette façon, en utilisant la méthode dite du Cube (présente dans le package BalancedSampling de R). Si l’on compare cette méthode par rapport à une sélection complètement au hasard des bureaux, on obtient les résultats suivants en termes d’erreur possible autour de la vraie valeur :
| Score Macron | Score Lepen | |
|---|---|---|
| Sondage équilibré | ± 1,10% | ± 1,51% |
| Sondage simple | ± 1,52% | ± 2,24% |
On gagne donc bien à mobiliser l’information de la précédente élection par équilibrage. Cependant, on peut aussi l’utiliser dans un second temps, par exemple par des redressements sur les résultats obtenus. De plus, dans mes simulations, j’ai négligé plusieurs paramètres :
Dans tous les cas, cette approche semble intéressante ! On voit que certains instituts ont eu des prédictions assez éloignées du score final (par exemple la prédiction sur TF1, l’image tout en haut de l’article), et cette méthode pourrait permettre de limiter ces erreurs.
Si cette élection présidentielle aura permis quelque chose, c’est bien d’avoir des discussions intéressantes sur les sondages ! Cette course à quatre est inédite dans l’histoire de la Vème République, et avec les grosses surprises de l’actualité récente (Trump et Brexit), il est normal de s’interroger sur l’incertitude réelle contenue dans ces données de sondages. Je propose donc de parler aujourd’hui des “marges d’erreurs” (dits aussi “intervalles de confiance à 95%”) qui ont pour but de quantifier cette incertitude. Je proposerai aussi une idée pour estimer une marge d’erreur prenant en compte à la fois les sondages (“le plan”) et l’évolution du paysage politique (“le modèle”).
Commençons par le début : aujourd’hui, on utilise une formule simple pour estimer les marges d’erreur d’un sondage : on prend le chiffre estimé et on effectue +/- deux fois l’erreur-type du sondage aléatoire simple de même taille. Malheureusement, ce mode de calcul ne repose sur aucun socle mathématique. La méthode utilisée par les instituts français, le sondage par quotas est en réalité très éloigné d’un sondage à probabilités égales, et les marges d’erreurs calculées ainsi ne correspondent pas à grand chose. C’est embêtant pour deux raisons qui peuvent sembler contradictoire :
– l’erreur aléatoire du sondage par quotas est probablement plus faible que celle utilisée pour calculer les marges (ce qui a amené des débats sur le “herding”)
– l’erreur totale est sans nul doute plus forte, car elle contient d’autres termes en plus de l’aléatoire (“vote caché”, profils difficiles à joindre, formulation des questions non neutres, etc.)
En plus de ces erreurs de mesure, on comprend bien que l’intention de vote sous-jacente des électeurs peut être elle-même variable ! Pour comprendre mieux ce dont on est en train de parler, on peut utiliser la formalisation suivante, empruntée à Binder et Roberts et illustrer avec le sondage politique :
Chaque observation à un instant t des intentions de vote consiste en un sondage en deux phases :
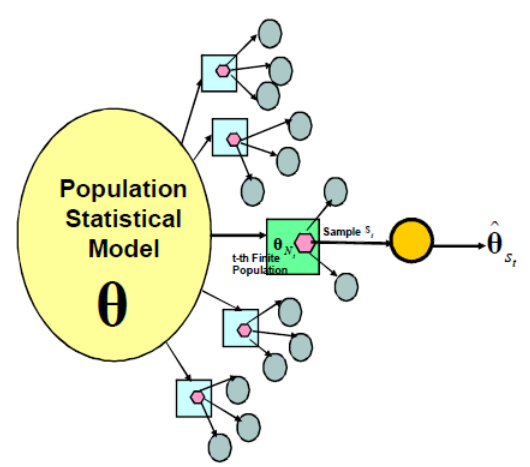
Notez que l’avantage de la formalisation en deux phases choisie ici est que l’on a :
Erreur totale = Erreur modèle + Erreur de sondage
Pour le deuxième terme, faute de mieux, on va conserver l’erreur de sondage telle qu’elle est calculée aujourd’hui (avec la formule du sondage aléatoire simple) : elle sur-estime l’erreur aléatoire mais ça n’est pas plus mal car cela permet de prendre en compte au moins en partie l’erreur de mesure (voir ce post qui en parle de façon plus détaillée)
Le premier terme est le plus intéressant ! Une idée très simple pour prendre en compte le modèle et l’erreur de sondage : mettre à profit les deuxièmes choix des électeurs, information que l’on retrouve dans un certain nombre d’enquêtes cette année (par exemple chez Ipsos, en page 11 de ce document). L’idée est que si des événements se produisent qui peuvent faire évoluer les intentions de vote, les électeurs auront tendance à se reporter sur leur deuxième choix plutôt que de changer totalement d’avis. Petite remarque : il faut bien intégrer dans ces choix potentiels la possibilité de l’abstention ou du vote blanc, qui ont bien entendu une influence sur la précision des estimations.
Cette idée permettrait d’intégrer la composante modèle à peu de frais ! Reste bien sûr la question de la quantification, mais je me dis que des règles naïves peuvent suffire à obtenir des estimations d’erreur de bonne qualité. Je serais très curieux de savoir si une définition pareille permet de construire des intervalles de confiance avec de bonnes propriétés de couverture. Je crains cependant que les données de deuxième choix des candidats soient peu disponibles pour les présidentielles précédentes.
Le modèle de “Too close to call” prend justement en compte ces information, et obtient des marges d’erreur très intéressantes :
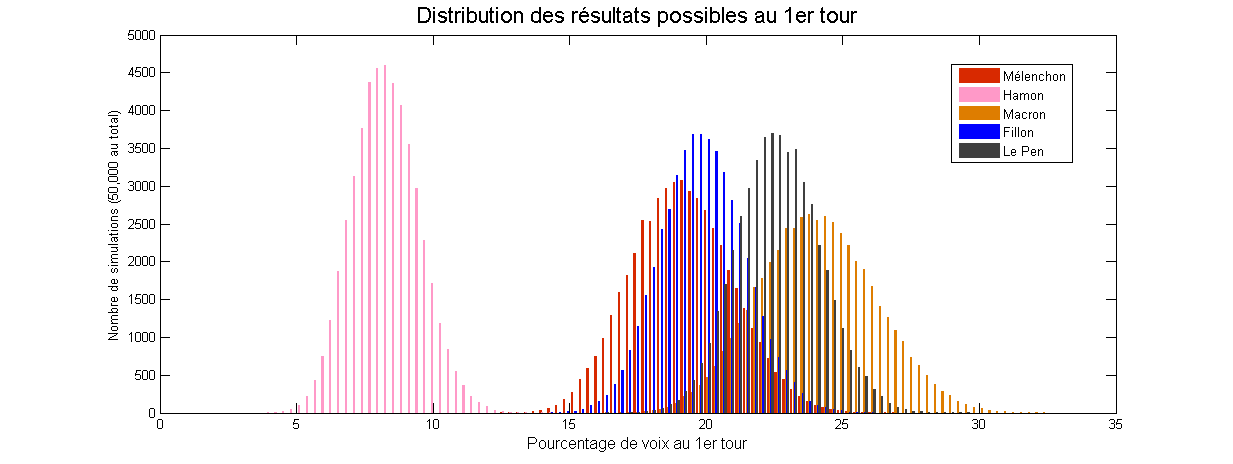
Ces marges reflètent en particulier la relative “sûreté” du score de Marine Le Pen, qui semble posséder une base fidèle ; le score d’Emmanuel Macron semble lui beaucoup plus incertain.
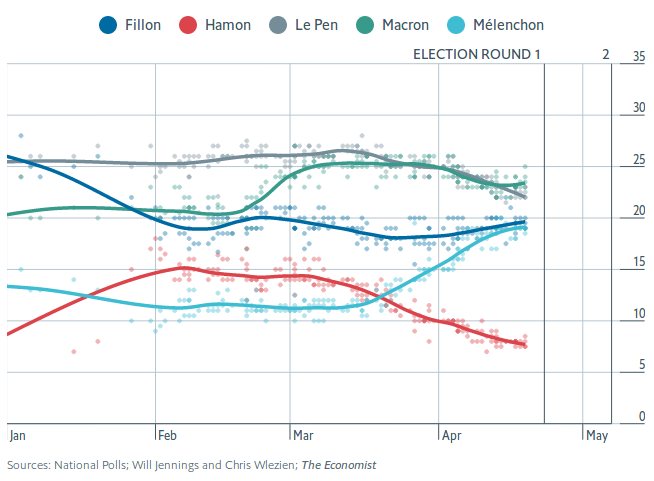
Un tweet de Nate Silver posté ce lundi semble avoir déchaîné les passions de nombreux observateurs :
I continue to worry about the lack of variation in French election polls. Polls shouldn't be this consistent unless there's massive herding. pic.twitter.com/Xgd8dNUytN
— Nate Silver (@NateSilver538) April 17, 2017
Dans ce gazouillis, Nate Silver (célèbre analyste statistique américain, rédacteur en chef du site fivethirtyeight.com) remarque que les estimations des intentions de vote par les instituts de sondage français sont assez proches les unes des autres, et suggère que cela est dû au fait que les sondeurs se “copient” les uns les autres (afin de limiter le risque d’être le seul institut proposant un résultat très éloigné du score final). Il nomme ceci le herding.
Un article publié dans The Economist hier lui emboîte le pas en s’intéressant notamment au cas de l’estimation du score de Marine Le Pen. Les autres tentent de montrer que la corrélation qu’on observe entre les différents résultats est improbable au sens statistique du terme, et en concluent qu’il y a nécessairement une intervention.
J’ai quelques doutes sur la validité de cette analyse.
L’erreur totale des sondages est composée de deux termes :
Erreur totale de mesure = Erreur d’échantillonnage + Erreur d’observation
Ainsi, l’étonnement des auteurs concerne l’erreur aléatoire d’échantillonnage – et c’est bien celle qui est considérée dans leur “test statistique”.
Pour un sondage américain typique, la réflexion fonctionne très bien car l’erreur d’échantillonnage estimée en utilisant la formule du sondage aléatoire simple est en général une sous-estimation de l’erreur d’échantillonnage réelle. L’article original de Nate Silver sur le herding est convainquant à cet égard.
Pour un sondage politique français, c’est beaucoup plus compliqué car les méthodes utilisées (notamment les quotas et l’utilisation intensive de redressements) sont très différentes des méthodes américaines ! La méthode des quotas et le redressement permettent, lorsque les variables mises en jeu (âge, géographie, catégorie socio-professionnelle et vote passé principalement) expliquent correctement le phénomène mesuré (les intentions de vote pour dimanche), de réduire sensiblement l’erreur d’échantillonnage.
De plus, j’ai “l’intuition” que le mode de sélection par quotas et le redressement (qui ne sont en fait pas aléatoire) peuvent eux-mêmes conduire à une corrélation des erreurs d’échantillonnage entre les instituts. J’espère vraiment avoir l’occasion dans des travaux futurs de proposer un modèle pour pouvoir tester cette idée ! La littérature sur les sondages par quotas est très peu développée et on ne peut que le regretter.
Ces deux arguments montrent que la variabilité des sondages “attendue” par les auteurs de l’article de The Economist est peut-être bien plus importante que leur variabilité réelle. Leur “probabilité” estimée que les sondages n’aient pas subi d’intervention est donc à mon avis très largement surestimée, et leur conclusion me semble hâtive.
Autrement dit à propos de leur méthodologie : le fait que peu de sondages sortent des marges d’erreur ne montre pas nécessairement que les sondeurs “trichent”, mais tout simplement… que leurs marges d’erreur sont mal calculées !
Il reste que cette corrélation entre les résultats est à double tranchant. Rien ne garantit que l’erreur totale des sondages français est inférieure à l’erreur totale des sondages américains. En résumé, la méthode française est sans doute plus risquée : il y a des chances que les résultats soient plus précis qu’avec la méthode “américaine”, mais en contrepartie, s’il y a une erreur, tous les sondages seront éloignés de la réalité à la fois ! Etant donné que la course à quatre de cette année est inédite dans l’histoire de la Vème République, rien ne garantit que l’on n’ait pas une grosse surprise dimanche à 20h !
A bientôt pour un post sur les marges d’erreur en sondages politique !
Illustrations : graphiques de l’article de The Economist, par Will Jennings et Chris Wlezien. Je ne possède pas les droits de ces images.
Tomorrow (march 23rd), I’ll be presenting my work on sampling designs for graph (and particularly extension sampling designs, with an application to Twitter data) at the MAD Stat seminar of the Toulouse School of Economics. Here are my slides:
This weekend I released version 0.3.0 of the Icarus package to CRAN.
Icarus provides tools to help perform calibration on margins, which is a very important method in sampling. One of these days I’ll write a blog post explaining calibration on margins! In the meantime if you want to learn more, you can read our course on calibration (in French) or the original paper of Deville and Sarndal (1992). Shortly said, calibration computes new sampling weights so that the sampling estimates match totals we already know thanks to another source (census, typically).
In the industry, one of the most widely used software for performing calibration on margins is the SAS macro Calmar developed at INSEE. Icarus is designed with the typical Calmar user in mind if s/he whishes to find a direct equivalent in R. The format expected by Icarus for the margins and the variables is directly inspired by Calmar’s (wiki and example here). Icarus also provides the same kind of graphs and stats aimed at helping statisticians understand the quality of their data and estimates (especially on domains), and in general be able to understand and explain the reweighting process.
I hope I find soon the time to finish a full well documented article to submit to a journal and set it as a vignette on CRAN. For now, here are the slides (in French, again) I presented at the “colloque francophone sondages” in Gatineau last october: https://nc233.com/icarus.
Kudos to the CRAN team for their amazing work!
There are many things I don’t like with so-called math reasoning and lotteries, and I wanted to write about it for a very long time. So, on the one hand we have the classic scammers who try to sell you the “most probable numbers” (or alternatively the “numbers that are due”). Of course, neither strategy is mathematically valid (because the draws are independent). On the other hand, many “educated” and “rational” people argue that, given that the expected value of a lottery ticket is negative (because the probability of wining a prize at the lottery is very low), smart people should never buy lottery tickets.
Now what if we could find a (mathematically correct!) strategy to make the expected value of our ticket positive? The idea is to choose the numbers that other players choose the least often, so that when we win a prize, it will be divided among fewer other players. But will it be enough to make a significant difference?
Let’s consider a lottery where players have to choose 6 numbers out of 19. The total number of players is 10000. The favorite numbers of the players are 1, 2, 3, 4, 5 and the least favorite are 15, 16, 17, 18, 19. They are respectively selected 2 times more often and 2 times less often than the other numbers 6 – 14. The company who runs the lottery decides to give the players back 90 percent of the amount of the tickets (thus ensuring a 10% profit) depending on the number of numbers they have chosen that also are in the right combination:
Then we compute the expected value for each ticket that was bought. You can find the R code I used on my GitHub page. I plotted the expected gains against an indicator of the rarity of the combination chosen by each player (the harmonic mean of the inclusion probabilities):
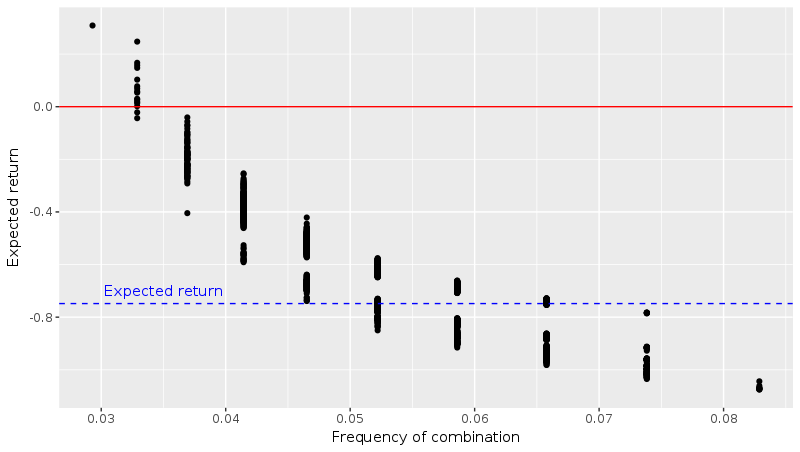
As we predicted, the expected gains are higher if you chose an “unpopular” combination. But what impresses me most is the order of magnitude of the effect. It is indeed possible to find a combination that yields a positive expected value (points on the left that are above the red line)!
I have no idea how all this works when we change the parameters of the problem: numbers to choose from (49 in France for example), number of players, choices of the players (inclusion probabilities of the numbers), payoffs, etc. I bet that the shape of the curve remains the same, but I wonder how high the expected value can get for the rarest combinations, and if it is always possible to find a winning strategy. I might try to work on an analytical solution when I find some time because I believe it involves some sampling theory.
Finally, a question to all people who never play the lottery because the expected value is negative, would you start buying tickets now that you know there exists a strategy with positive expected value?

PS: Henri pointed out chapter 11 of Jordan Ellenberg’s “How not to be wrong” which deals with interesting mathematical facts about the lottery, including a similar discussion as this post. Be sure to check it out, it’s really great!