Author: Antoine Rebecq

Après un été chargé en sports, l’automne et la Ligue 1 reprennent peu à peu leurs droits. C’est l’occasion de détailler un sujet d’analyse de données élaboré pour un cours à l’ENSAE. Il s’agit d’analyser des données qualitatives (caractéristiques physiques, tactiques et aptitudes relatives à certains aspects techniques du jeu) décrivant les joueurs du championnat de France de football. Le but final est de déterminer “statistiquement” à quel poste faire jouer Mathieu Valbuena 🙂 On utilise le langage R et l’excellent package d’analyse de données FactoMineR.

Les données

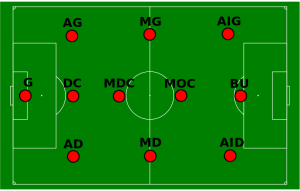
Comme indiqué dans l’énoncé du TD, il n’est pas nécessaire de bien connaître le football pour pouvoir suivre cet article. Seule une notion de l’emplacement des joueurs sur le terrain en fonction de leur poste (correspondant à la colonne “position” du dataset) est souhaitable. Voici un petit schéma pour aider les moins avertis :

Les données sont issues du jeu vidéo Fifa 15 (les connaisseurs auront remarqué que les données datent donc d’il y a déjà deux saisons, il peut donc y avoir quelques différences avec les effectifs actuels !), qui donne de nombreuses statistiques pour chaque joueur, incluant une évaluation de leurs capacités. Les données de Fifa sont quantitatives (par exemple chaque capacité est notée sur 100) mais pour cet article on les a rendues catégorielles sur 4 positions : 1. Faible / 2. Moyen / 3. Fort / 4. Très fort. On verra l’intérêt d’avoir procédé ainsi un peu plus loin !

Préparation des données

Commençons par charger les données. Notez l’utilisation de l’option stringsAsFactors=TRUE (plus d’explications sur ce fameux paramètre stringsAsFactors ici). Eh oui, une fois n’est pas coutume, FactoMineR utilise des facteurs pour effectuer l’analyse de données !

> champFrance <- read.csv2("td3_donnees.csv", stringsAsFactors=TRUE)
> champFrance <- as.data.frame(apply(champFrance, 2, factor))

La deuxième ligne sert à transformer les colonnes de type int créés par read.csv2 en factors.

FactoMineR utilise le paramètre “row.names” des data.frame de R pour l’affichage sur les graphes. On va donc indiquer qu’il faut utiliser la colonne “nom” en tant que row.names pour faciliter la lecture :

> row.names(champFrance) <- champFrance$nom
> champFrance$nom <- NULL

Voilà à quoi ressemble désormais notre data.frame (seules les premières lignes sont affichées) :

> head(champFrance)
                      pied position championnat age taille general
Florian Thauvin     Gauche      MDR      Ligue1   1      3       4
Layvin Kurzawa      Gauche       AG      Ligue1   1      3       4
Anthony Martial      Droit       BU      Ligue1   1      3       4
Clinton N'Jie        Droit       BU      Ligue1   1      2       3
Marco Verratti       Droit       MC      Ligue1   1      1       4
Alexandre Lacazette  Droit       BU      Ligue1   2      2       4

Analyse des données

Nous avons affaire à un tableau de variables catégorielles : la méthode adaptée est l’Analyse des Correspondances Multiples, qui est implémentée dans FactoMineR par la méthode MCA. Pour le moment on exclut de l’analyse les variables “position”, “championnat” et “âge” (que l’on traite comme variables supplémentaires) :

> library(FactoMineR)
> acm <- MCA(champFrance, quali.sup=c(2,3,4))

Trois graphes apparaissent dans la sortie : la projection sur les deux premiers axes factoriels des catégories et des individus, ainsi que le graphe des variables. A ce stade, seul le second nous intéresse :

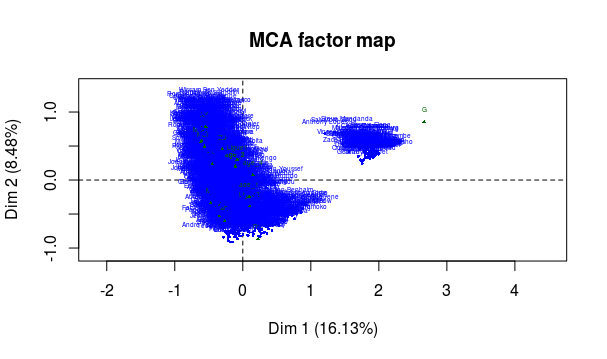
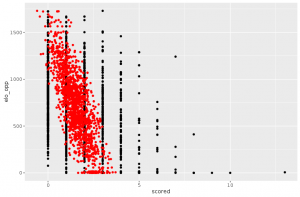
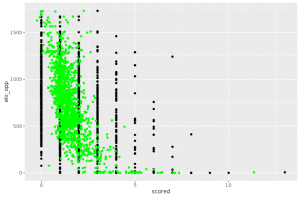
Avant même d’essayer d’aller plus loin dans l’analyse, quelque chose doit nous sauter aux yeux : il y a clairement deux nuages de points ! Or nos méthodes d’analyse de données supposent que le nuage qu’on analyse est homogène. Il va donc falloir se restreindre à l’analyse de l’un des deux nuages que l’on observe sur ce graphe.

Pour identifier à quels individus le nuage de droite correspond, on peut utiliser les variables supplémentaires (points verts). On observe que la projection de la position goal (“G”) correspond bien au nuage. En regardant de plus près les noms des individus concernés, on confirme que ce sont tous des gardiens de but.

On va se concentrer pour le reste de l’article sur les joueurs de champ. On en profite également pour retirer les colonnes ne concernant que les capacités de gardien, qui ne sont pas importantes pour les joueurs de champ et ne peuvent que bruiter notre analyse :

> champFrance_nogoals <- champFrance[champFrance$position!="G",-c(31:35)]
> acm_nogoals <- MCA(champFrance_nogoals, quali.sup=c(2,3,4))

Et l’on vérifie bien dans la sortie graphique que l’on a un nuage de points homogène.

Interprétation

On commence par réduire notre analyse à un certain nombre d’axes factoriels. Ma méthode favorite est la “règle du coude” : sur le graphe des valeurs propres, on va observer un décrochement (le “coude”) suivi d’une décroissance régulière. On sélectionnera ensuite un nombre d’axes correspondant au nombre de valeurs propres précédant le décrochement :

> barplot(acm_nogoals$eig$eigenvalue)

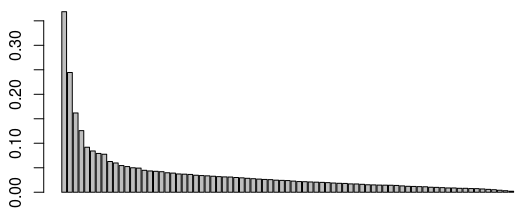
Ici, on peut choisir par exemple 3 axes (mais on pourrait justifier aussi de retenir 4 axes). Passons maintenant à l’interprétation, en commençant par les graphes des projections sur les deux premiers axes retenus pour l’étude.

> plot.MCA(acm_nogoals, invisible = c("ind","quali.sup"))

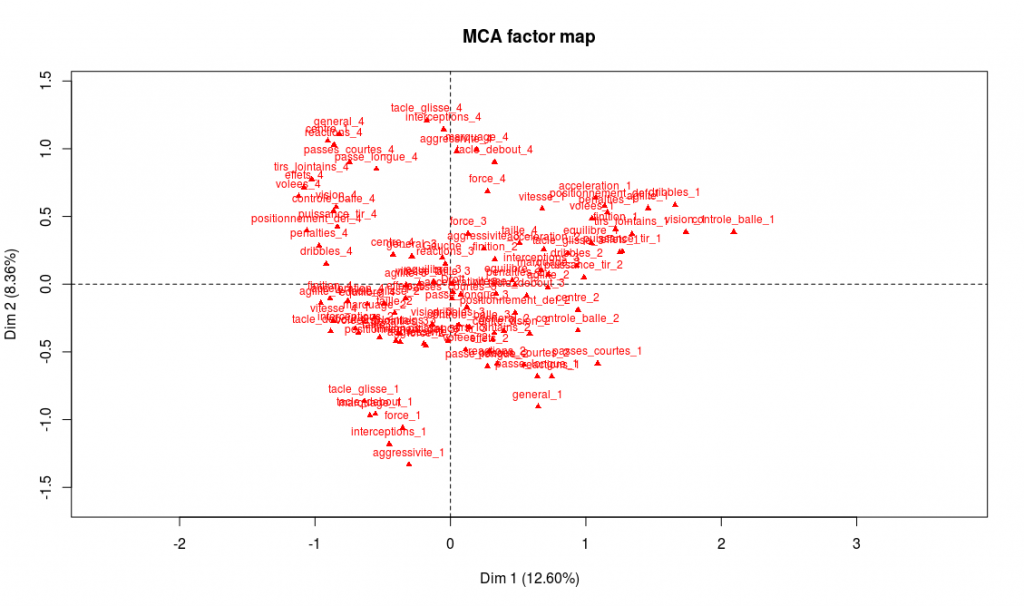
On peut par exemple lire sur ce graphe le nom des modalités possédant les plus fortes coordonnées sur les axes 1 et 2 et commencer ainsi l’interprétation. Mais avec un tel de nombre de modalités, la lecture directe sur le graphe n’est pas si aisée. On peut également obtenir un résultat dans la sortie texte spécifique de FactoMineR, dimdesc (seule une partie de la sortie est donnée ici) :

> dimdesc(acm_nogoals)

$`Dim 1`$category
                         Estimate       p.value
finition_1            0.700971584 1.479410e-130
volees_1              0.732349045 8.416993e-125
tirs_lointains_1      0.776647500 4.137268e-111
tacle_glisse_3        0.591937236 1.575750e-106
effets_1              0.740271243  1.731238e-87
[...]
finition_4           -0.578170467  7.661923e-82
puissance_tir_4      -0.719591411  2.936483e-86
controle_balle_4     -0.874377431 5.088935e-104
dribbles_4           -0.820552850 1.795628e-117

Les modalités les plus caractéristiques de l’axe 1 sont, à droite, un niveau faible dans les capacités offensives (finition, volées, tirs lointains), et de l’autre un niveau très fort dans ces même capacités. L’interprétation naturelle est donc que l’axe 1 discrimine selon les capacités offensives (les meilleurs attaquants à gauche, les moins bons à droite). On procède de même pour l’axe 2, et on observe le même phénomène, mais avec les capacités défensives : en haut on trouvera les meilleurs défenseurs, et en bas les moins bons défenseurs.

Les variables supplémentaires peuvent aussi aider à l’interprétation, et vont confirmer notre interprétation, notamment la variable de position :

> plot.MCA(acm_nogoals, invisible = c("ind","var"))

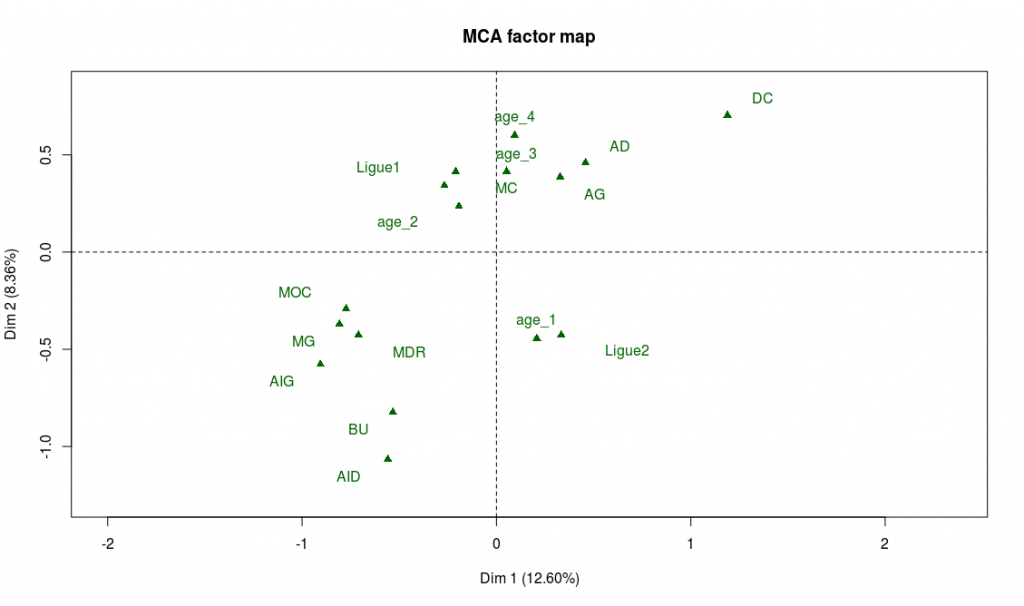
On trouve bien à gauche du graphe les les postes offensifs (BU, AIG, AID) et en haut les postes défensifs (DC, AD, AG).

Une conséquence de cette interprétation est que l’on risque de trouver les joueurs de meilleur niveau organisés le long de la seconde bissectrice, avec les meilleurs joueurs dans le quadrant en haut à gauche, et les plus faibles dans le quadrant en bas à droite. Il y a beaucoup de moyens de le vérifier, mais on va se contenter de regarder dans le graphe des modalités l’emplacement des observations de la variable “général”, qui résume le niveau d’un joueur. Comme on s’y attend, on trouve “général_4” dans en haut à gauche et “général_1” dans le quadrant en bas à droite. On peut observer aussi le placement des variables supplémentaires “Ligue 1” et “Ligue 2” pour s’en convaincre 🙂

A ce stade, il y a déjà plein de choses intéressantes à relever ! Parmi celles qui m’amusent le plus :

• Les ailiers gauches semblent avoir un meilleur niveau que les ailiers droits (si un spécialiste du foot voulait bien m’en expliquer la raison ce serait top !)
• L’âge n’est pas explicatif du niveau du joueur, sauf pour les plus jeunes qui ont un niveau plus faible
• Les joueurs les plus âgés ont des rôles plus défensifs.

N’oublions pas de nous occuper de l’axe 3 :

> plot.MCA(acm_nogoals, invisible = c("ind","var"), axes=c(2,3))

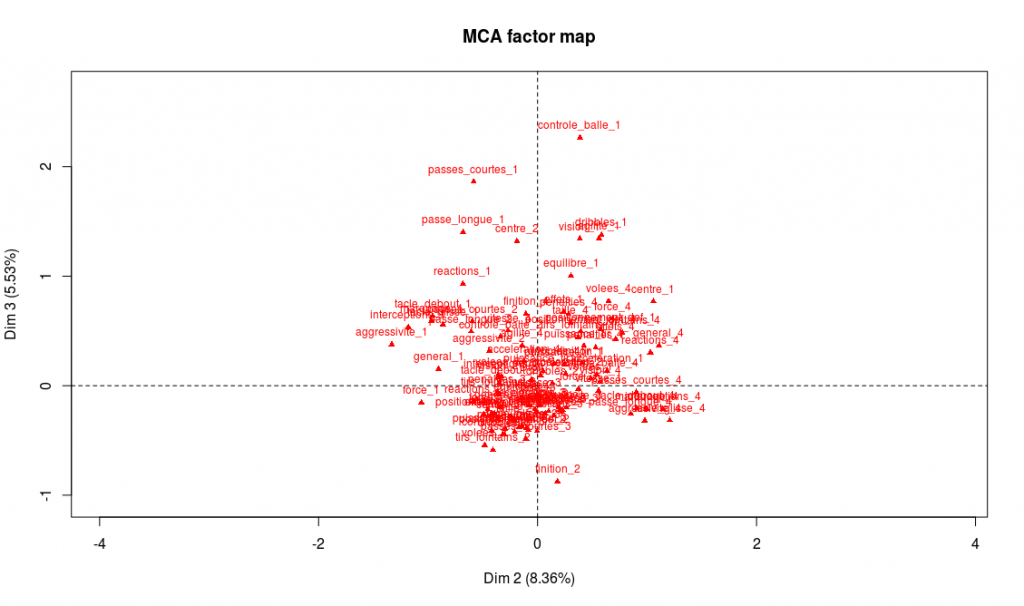
Les modalités les plus caractéristiques de ce troisième axe sont les faiblesses techniques : les joueurs les moins techniques sont sur les extrémités de l’axe, et les joueurs les plus techniques au centre. On le confirme sur le graphe des variables supplémentaires : les buteurs et défenseurs centraux sont en effet moins réputés pour leurs capacités techniques, tandis que tous les postes de milieux se retrouvent au centre de l’axe :

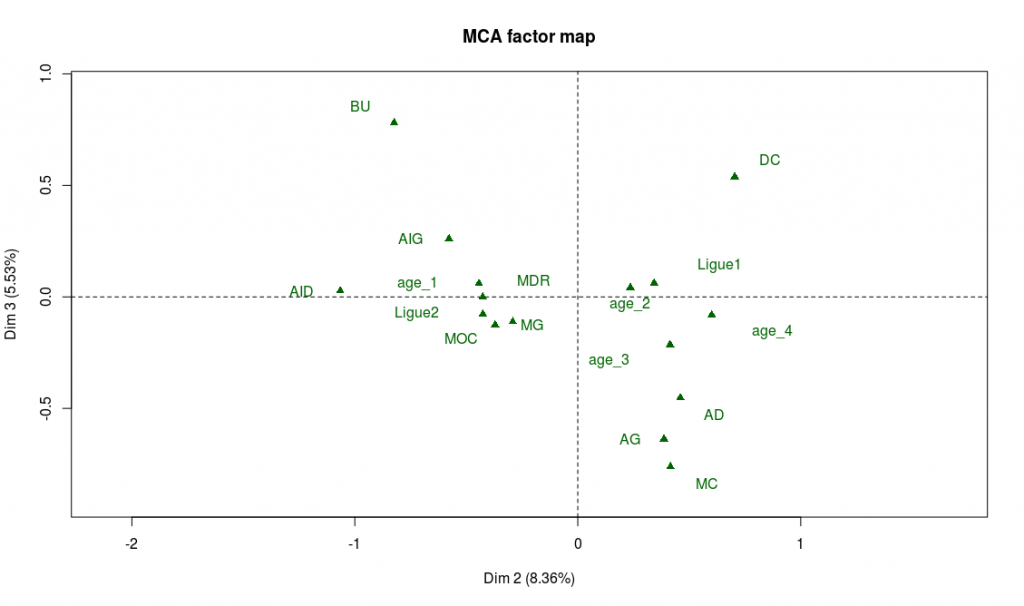
C’est l’intérêt d’avoir rendu ces variables catégorielles. Si l’on avait conservé le caractère quantitatif des données originelles de Fifa et effectué une ACP, les projections de chaque caractéristique sur chaque axe auraient été ordonnées par niveau, contrairement à ce qui se passe sur l’axe 3. Et après tout, discriminer les joueurs suivant leur niveau technique ne reflète pas forcément toute la richesse du football : à certains postes, on a besoin de techniciens, mais à d’autres, on préférera des qualités physiques !

Mathieu Valbuena

On va maintenant ajouter les données d’un nouvel entrant dans le championnat de France : Mathieu Valbuna (oui je vous avais prévenu, les données commencent à dater un peu :p) et le comparer aux autres joueurs en utilisant notre analyse.

> columns_valbuena <- c("Droit","AID","Ligue1",3,1
 ,4,4,3,4,3,4,4,4,4,4,3,4,4,3,3,1,3,2,1,3,4,3,1,1,1)
> champFrance_nogoals["Mathieu Valbuena",] <- columns_valbuena

> acm_valbuena <- MCA(champFrance_nogoals, quali.sup=c(2,3,4), ind.sup=912)
> plot.MCA(acm_valbuena, invisible = c("var","ind"), col.quali.sup = "red", col.ind.sup="darkblue")
> plot.MCA(acm_valbuena, invisible = c("var","ind"), col.quali.sup = "red", col.ind.sup="darkblue", axes=c(2,3))

Les deux dernières lignes permettent de représenter Mathieu Valbuena sur les axes 1 et 2, puis 2 et 3 :

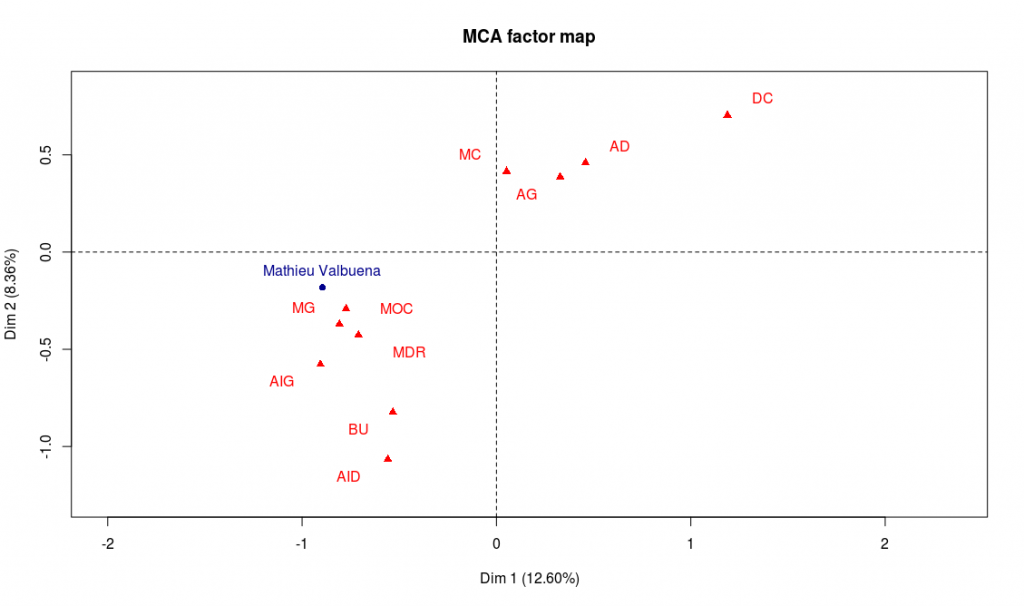
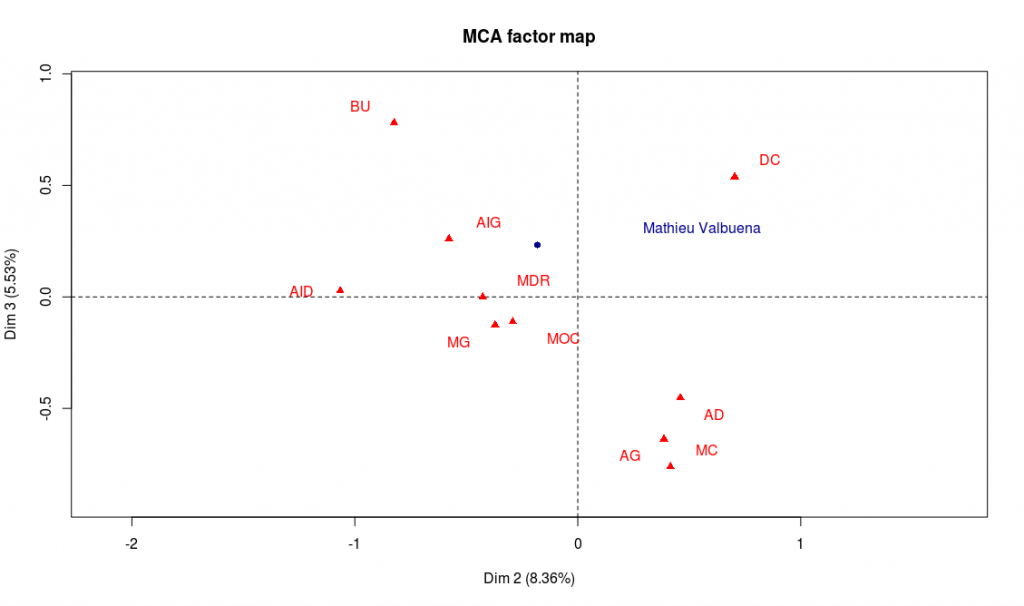
Résultat de notre analyse : Mathieu Valbuena a plutôt un profil offensif (gauche de l’axe 1), mais possède un bon niveau général (sa projection sur la deuxième bissectrice est assez élevée). Il possède également de bonnes aptitudes techniques (centre de l’axe 3). Enfin, ses qualités semblent plutôt bien convenir aux postes de milieu offensif (MOC) ou milieu gauche (MG). Avec quelques lignes de code, on peut trouver les joueurs du championnat dont le profil est le plus proche de celui de Valbuena :

> acm_valbuena_distance <- MCA(champFrance_nogoals[,-c(3,4)], quali.sup=c(2), ind.sup=912, ncp = 79)
> distancesValbuena <- as.data.frame(acm_valbuena_distance$ind$coord)
> distancesValbuena[912, ] <- acm_valbuena_distance$ind.sup$coord

> euclidianDistance <- function(x,y) {
 
 return( dist(rbind(x, y)) )
 
}

> distancesValbuena$distance_valbuena <- apply(distancesValbuena, 1, euclidianDistance, y=acm_valbuena_distance$ind.sup$coord)
> distancesValbuena <- distancesValbuena[order(distancesValbuena$distance_valbuena),]

# On regarde les profils des 5 individus les plus proches
> nomsProchesValbuena <- c("Mathieu Valbuena", row.names(distancesValbuena[2:6,]))

Et l’on obtient : Ladislas Douniama, Frédéric Sammaritano, Florian Thauvin, N’Golo Kanté et Wissam Ben Yedder.

Il y aurait plein d’autres choses à dire sur ce jeu de données mais je préfère arrêter là cet article déjà bien long 😉 Pour finir, gardez à l’esprit que cette analyse n’est pas vraiment sérieuse et sert surtout à présenter un exemple sympathique pour la découverte de FactoMineR et de l’ADD.