Comme certains ont pu le dire à l’époque des débats sur le mariage gay, en 2012, il y avait une crainte que cette nouvelle loi amène l’apocalypse et la fin de la civilisation en France. Il semblerait que, deux ans et quelques jours après, l’apocalypse ne soit pas encore arrivée, et que seuls quelques dizaines de milliers de mariage aient été célébrés. Mais on n’en est qu’à deux ans après l’adoption de la loi : que pourrait-il bien se passer à plus long terme ?
Pour éviter de recevoir trop de mails d’insultes et autres réjouissances, je vais vous rassurer de suite : il ne s’agira pas dans cet article de s’intéresser à l’impact sur les enfants, la société, ou que sais-je, du fait d’avoir autorisé deux hommes ou deux femmes à se marier. Non, ce qui m’a frappé dans cette loi, c’est son article 11. Celui-ci dit :
« En cas de désaccord entre les parents, signalé par l’un d’eux à l’officier de l’état civil, au plus tard au jour de la déclaration de naissance ou après la naissance, lors de l’établissement simultané de la filiation, l’enfant prend leurs deux noms, dans la limite du premier nom de famille pour chacun d’eux, accolés selon l’ordre alphabétique. »
Je résume (sans aucune mauvaise foi) : blablabla, le nom des enfants sera celui des parents accolés dans l’ordre alphabétique. C’est bien, l’ordre alphabétique, non ? C’est neutre, c’est pour l’égalité homme-femme, homme-homme et femme-femme, tout ça. Mais ce qui me perturbe, personnellement, c’est que si monsieur A épouse madame B (+1 point hétérocentrisme), leurs enfants s’appelleront A-B. Et si ils épousent les enfants de C et D, soient les C-D, eh bien leurs enfants à eux (les petits-enfants de monsieur A et madame B) auront A-C comme patronyme. Vous avez bien vu, les noms de famille B et D ont disparu. Pourquoi ? Parce qu’ils sont plus loin dans l’ordre alphabétique. Le mariage va donc bien détruire notre civilisation, en s’attaquant à nos patronymes ! Peut-on essayer d’évaluer la vitesse de cette décadence ?
Quelle sont les noms de famille les plus courants ?
La question du nom de famille le plus courant n’est pas compliquée : c’est Martin, avec une très large avance. Certains sites comme celui-ci permettent de le savoir, bien que leurs sources ne soient pas très clairement précisées. Mais ce qui nous intéresse ici est une distribution plus générale des noms de famille en France. Pour cela, nous allons utiliser les données du Bac 2014, en faisant des statistiques sur les noms des candidats. Cela peut créer quelques biais, parce que cela concerne une seule génération et non pas la population toute entière, et parce que toute la génération en question ne se présente pas au bac (qu’il soit général, professionnel ou technologique). Néanmoins, c’est une des sources les plus solides pour ce genre de questions, d’autant plus que leur âge uniforme (et leur absence d’enfants, a priori) va permettre de les considérer comme la première génération. La distribution, rapportée à 10.000 personnes, est la suivante :
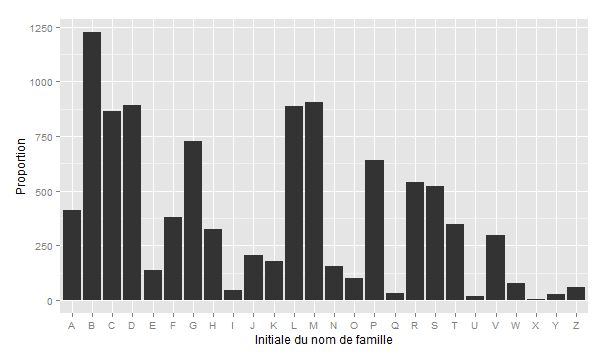
On a représenté la distribution des noms de famille suivant les initiales. On remarque déjà que c’est la lettre B qui est la plus courante (vous connaissez beaucoup de personnes dont le nom de famille commence par B ? C’est normal), et qu’il y a de fortes disparités entre les différentes lettres : pas grand monde n’a un patronyme commençant par Q, U ou X, du moins en France.
Avec un peu de mauvaise foi
Maintenant que nous connaissons la situation initiale de la répartition des noms de famille en France, du moins de leurs initiales, il est temps de s’intéresser à l’impact qu’aurait le fait d’attribuer aux enfants les deux noms de leurs parents 1 et 2 (-1 point hétérocentrisme), ordonnés dans l’ordre alphabétique, dans la limite d’un nom par parent. Pour cela nous allons utiliser un modèle très simple de générations : parmi les N individus de notre population, les N/2 premiers vont se marier avec les N/2 autres, au hasard (du moins au hasard selon l’initiale du nom de famille, d’autres facteurs pouvant jouer). Ensuite, on va supposer que chacun des couples aura deux enfants : leurs noms de familles commenceront par l’initiale du nom des deux parents qui est le premier dans l’ordre alphabétique. Evidemment, comme le mariage gay est autorisé, on ne s’intéressera pas au sexe des marié(e)s : ils auront leurs enfants de la façon qui leur convient, cela n’est pas la question soulevée ici.
À quoi va ressembler la distribution des noms de familles dans la génération suivante, pour les bacheliers de 2040 ? Les simulations donnent le résultat suivant :
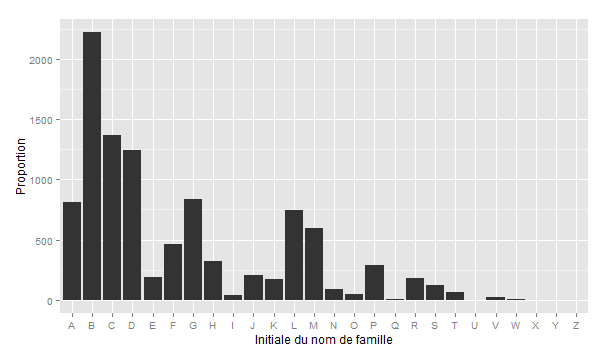
On remarque déjà une belle modification de la distribution des noms de famille. Beaucoup plus de personnes ont un nom qui commence par une lettre de début de l’alphabet, et c’est évidemment l’inverse pour les noms dans le milieu et la fin de l’alphabet. Mais la modification est encore mineure : que se passera t-il dans 5 générations, soit dans 125 ans environ ?
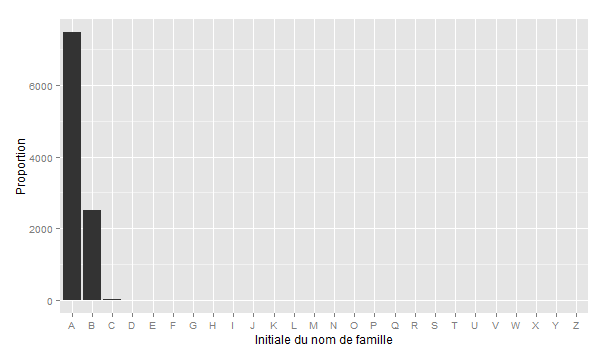
Impressionnant. La distribution n’a plus rien à voir : tous les patronymes commencent par A, B, voire C pour quelques chanceux. La totalité de la culture présente dans nos patronymes a été anéantie. C’est véritablement l’apocalypse annoncée.
Soyons plus réalistes
J’ai un peu joué sur les mots dans la partie précédente. L’article de loi ne force personne à donner comme nom de famille à ses enfants les deux noms de ses parents dans l’ordre alphabétique, elle donne seulement un cadre pour toute situation où il y aurait désaccord ou problème. Il s’agit donc d’appliquer cette règle uniquement dans ces cas. Nous évaluons à environ 10% des cas cette règle : que ce soit par erreur, par désaccord, pour éviter tout problème dans le couple, il nous semble crédible qu’un couple sur 10 environ suive la règle édictée par la loi. Pour les 90% autres, il y a un accord entre les parents : on peut raisonnablement penser que cet accord se fait la moitié du temps en faveur du parent 1, et la moitié du temps en faveur du parent 2 (-1 point hétérocentrisme, j’espère finir en négatif). Dans ce cas, l’évolution d’une génération à l’autre est évidemment moins marquée que dans le cas précédent. Mais que se passe t-il à long terme ?
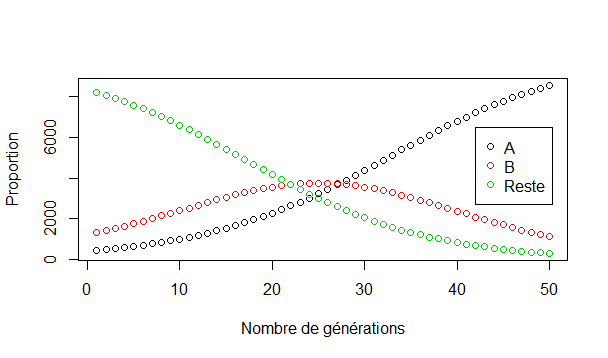
Ce (magnifique) graphe s’intéresse à l’évolution générale des initiales des noms de familles, entre ceux commençant par A, qui commencent à environ 4%, pour monter très haut génération après génération, ceux par B qui connaissent un pic aux alentours de la 25ème génération, tandis que toutes les autres lettres tendent à disparaître à plus ou moins long terme. Plus précisément, ce graphe dynamique montre l’évolution d’une génération à l’autre de la distribution des noms de famille :
Même avec des hypothèses plus réalistes, il n’y a que le délai avant l’apocalypse qui change. De manière plus précise, nous pouvons estimer à partir de combien de générations il n’y aura plus de noms commençant par chacune des lettres (sauf A, qui ne disparaît jamais, et B qui persiste de nombreuses générations) :
| C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
| 100 |
98 |
74 |
82 |
87 |
77 |
57 |
71 |
70 |
81 |
81 |
63 |
| O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
| 56 |
72 |
45 |
70 |
70 |
64 |
36 |
62 |
48 |
13 |
39 |
46 |
Légende : Sous chaque lettre est indiquée le nombre de générations nécessaires avant la disparition de la totalité des noms de famille commençant par cette lettre. Par exemple, il faut attendre 46 générations pour que tous les patronymes commençant par Z disparaissent.
Les noms en X sont les premiers à disparaître, après 13 générations, soit un peu plus de 3 siècles, ce qui nous laisse tout de même le temps de voir venir. Mais, en parlant de noms de famille commençant par X, vous en connaissez beaucoup ? Xavier, d’accord, mais à part celui-là ? La plupart d’entre eux sont des noms d’origine étrangère, et donc viennent de l’immigration. Ce qui est précisément le facteur que nous avons oublié.
L’immigration va-t-elle nous sauver ?
Il serait plus correct de dire l’un des deux facteurs : pour être tout à fait exact, il faudrait mentionner que pas tout le monde ne se marie et n’a des enfants, mais ce comportement n’a aucune raison d’être lié au nom de famille, du moins pas directement. On peut donc supposer que 15% des gens n’ont pas d’enfants (selon le Figaro, c’est un homme sur 5, mais à 50 ans ce qui laisse un peu de marge – on peut aussi aller jeter un oeil sur fivethirtyeight (en) sur la question aux États-Unis).
Mais revenons à l’immigration. Comme nous n’avons aucune envie de nous lancer dans le débat sur le nombre d’immigrés arrivant ou repartant, laissons ça aux spécialistes. Ce qui nous intéresse ici est une étude à long terme, et un modèle fréquemment utilisé en démographie pour cela est celui de population stationnaire, où la taille n’évolue plus. On va donc supposer que les 15% d’enfants qui ne sont pas nés d’après l’hypothèse précédente sont remplacés par une immigration entrante de même taille.
Reste une question de taille : si l’on s’intéresse aux noms de famille des personnes venant vivre en France, comment connaître leur répartition ? On pourrait imaginer récupérer des données sur l’ensemble des pays du monde, et les pondérer selon le pourcentage d’arrivants par pays, qui n’est pas très bien connu, en prenant en compte des évolutions pour chacune des générations successives. Mais c’est très compliqué, et cela n’aurait concrètement rien apporté de tangible. Nous allons nous limiter à deux hypothèses qui sont aussi peu crédibles l’une que l’autre, mais qui ont le bénéfice d’être simples à mettre en oeuvre.
Tout d’abord, supposons que la totalité des pays du monde a la même distribution des noms de famille que la France. Dans ce cas, les noms des immigrants suivent la même répartition que celle de la France avant l’application de la loi, c’est à dire celle des bacheliers 2014. L’évolution est alors la suivante :
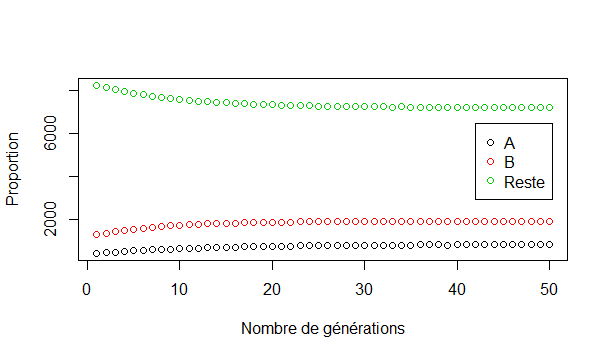
Une autre hypothèse est de dire que comme les noms de familles peuvent provenir de pays, de cultures et même d’alphabets très différents, il y a autant de chance que le nom de famille commence par chacune des lettres de l’alphabet latin. Autrement dit, la répartition des initiales des noms des arrivants est uniforme. L’évolution est alors la suivante :

Dans les deux cas, la situation ne semble plus se dégrader à moyen terme : les noms de familles commençant par toutes les lettres hormis les toutes les premières ne vont pas disparaître d’ici quelques siècles, bien qu’il y ait une légère hausse des noms commençant par A et B dans le cas d’une répartition des noms mondiale similaire à celle de la France. Cas très improbable, on le rappelle.
Il semblerait donc que l’immigration nous sauvera de l’apocalypse causée par l’adoption du mariage gay. Quel retournement de situation, n’est-ce pas ?
image source : Wikimedia, Le mariage de Sigebert Ier et de Brunehaut









![[Geekery] Dodging 9s](https://nc233.com/wp-content/uploads/2016/07/9_playing_cards-825x510.jpg)


![[Sampling] Combien de salons de coiffure ont un jeu de mots dans leur nom ? (Deuxième partie)](https://nc233.com/wp-content/uploads/2016/01/boulet_coiffure.png)
![[Geekery] Le mariage gay, une “loi détruisant notre société” ?](https://nc233.com/wp-content/uploads/2015/04/Mariage_de_Sigebert_Ier_et_Brunehaut-825x510.jpg)






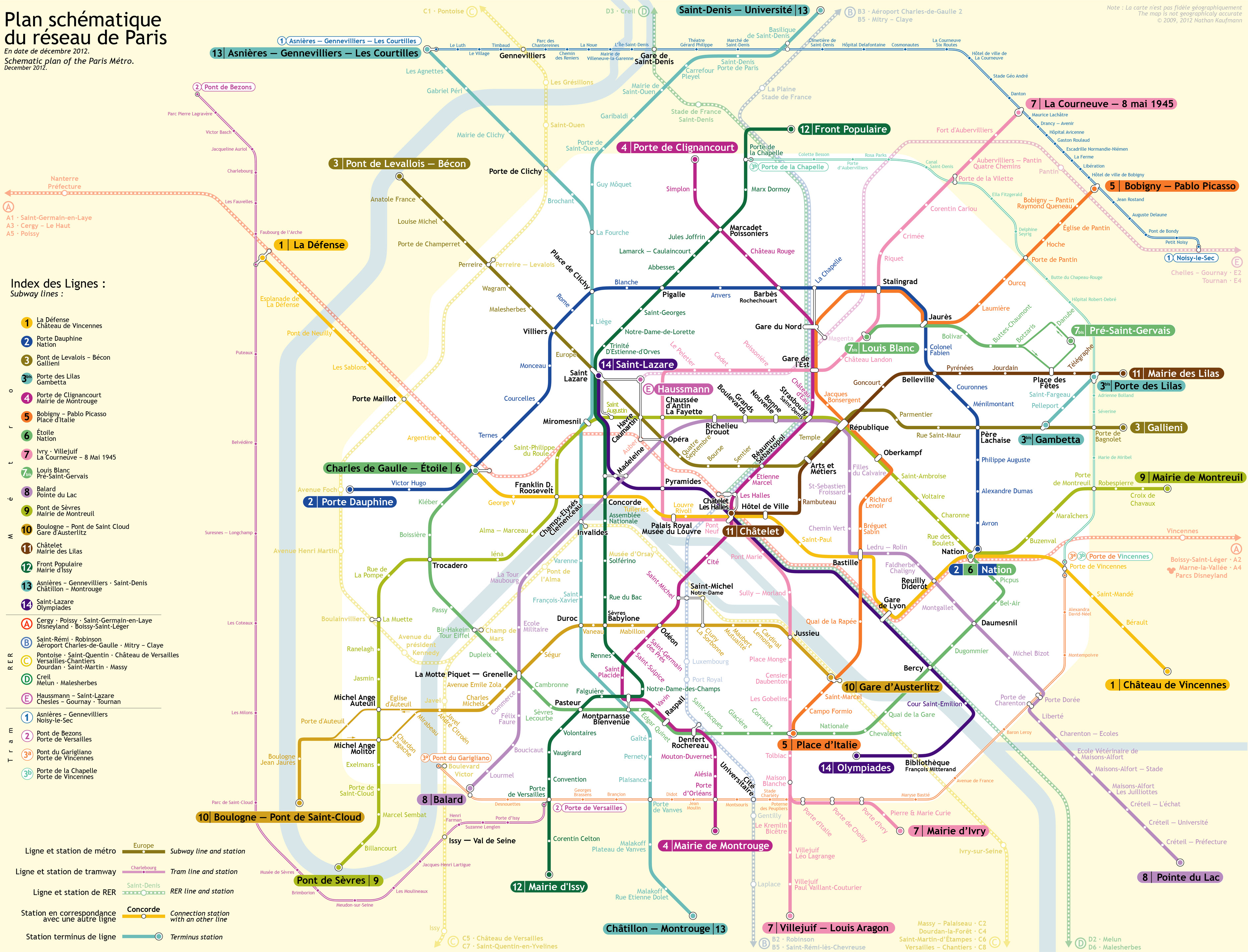
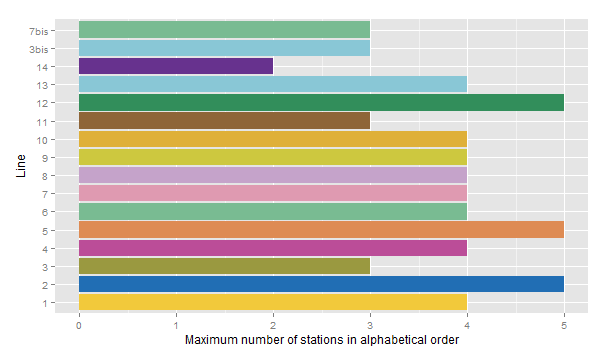
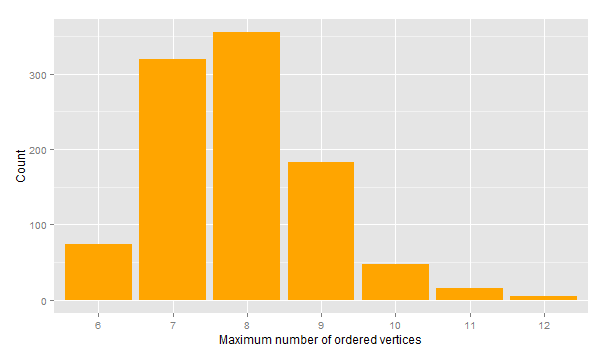
![[Geekery] How many stations of the Paris Métro could you pass through in alphabetical order?](https://nc233.com/wp-content/uploads/2015/03/Abesses_entrance_1-825x510.jpg)