Author: Thomas M

Creating an hex map of France electricity consumption

The French Ministry for the Ecological and Inclusive Transition (for which I’m currently working) is ongoing a process of opening data related to energy consumption. Each year, we publish data for every neighborhood in France (at the iris statistical level, even adresses in some cases) and to the nature of the final consumer (a household, an industry, a shop…). These data are available here (website in French – direct link to 2018 electricity consumption data).

Making a map to have an overlook at the situation isn’t easy, because the administrative boundaries of France are very diverse, and a direct mapping will reflect this situation. In order to overcome this issue, a solution is to use a different way to represent the country. In this post, we’re going to talk about hex map (as inspired by this website).

What’s a hex map? First, we need to talk about chloropleth maps; despite their unusual names, they’re perfectly common maps where each area is shaded or colored differently according to the values taking by a variable. They’re quite similar to maps such as this one showing which political party won an election on each voting district, but for continuous variable, and required a scale. To determine the color used for each area, we need to compute the average (or any statistical summary) of the values of every individual belonging in this area.

Hex map are entirely composed of hexagons (something perfectly suited for France!); they’re chloropleth maps, so each hexagon is colored depending on the values taking by a variable. The main difference is that the hexagon aren’t usual geographical areas so we need a way to attribute each value in our data set to one of the hexagons before calculating averages, and therefore colors.

In order to do that, we’re going to load some usual R-packages:

library(tidyverse)  
library(viridis)   
library(ggplot2)   
library(stringr)

Our objective will be to make an hex map of residential consumption of electricity in 2018. First, we need to import the data at iris level (doing this, we miss some of the electricity consumption only associated to larger geographical area, but it’s marginal); as the data is coded as strings with some missing values, we start by cleaning the data.

elec <- read.csv2("donnees_elec_iris_2018.csv",stringsAsFactors = F)
elec <- elec[elec$CONSO != "s" & elec$PDL != "s",] #"s" are missing values

# CONSO (electricity consumption) is coded with a french comma separator ; we need to substitute that and convert to numeric CONSO and PDL (number of  energy delivery points) 
elec$CONSO <- str_replace(elec$CONSO,",",".") 
elec$CONSO <- as.numeric(elec$CONSO)
elec$PDL <- as.numeric(elec$PDL)

# Select only residential sector
res <- elec[elec$CODE_GRAND_SECTEUR == "R",]

Each data point is then associated to the coordinates of the center of the neighborhood, using a iris shapefile (available here). The res dataset obtained looks like this:

  CODE_IRIS      CONSO  PDL     x    y
  100020000   843.8162  124 48.25 4.69
  100030000 10374.7166 1987 48.24 3.72
  100040000   679.8085   88 48.59 4.12
  100050000   769.8268  145 48.29 4.49
  100060000  7318.2055 1534 48.53 4.14
  100070000   429.9674   61 48.16 4.73
  100080000   343.1404   62 48.25 4.60
  100090000   262.1539   55 48.05 4.28
  100100000   140.5366   28 48.54 4.61
  100110000   700.1244  113 48.27 4.74

We’re using a ggplot2 environment to create our hex map. The aesthetics used are aes(x,y), the spatial coordinates. We begin by these line of code in order to use a simpler theme (as we’re creating a map, we don’t need any axis) and to specify the positions (longitude and latitude) we want to map.

c <- ggplot(res, aes(x, y))
c + 
xlim(-9, 12) +
ylim(40, 52) +   
theme_void()

The main argument of the stat_summary_hex function we’re going to use is bins. This parameter allows us to choose how many hexagons will be displayed on the map; the more hexagon, the more small local variations are shown. For the other parameters, we specify aes(z = CONSO) as we want to color the hexagons in relation to the CONSO (Consumption in french) of the data points contained in this area. The fun = “sum” parameter means that the choice of the color of the hexagon depends on the total consumption inside. Lastly, we add a colour=”grey” parameter, which defines the color of every hexagon’s borders, because using white borders on my computer leads to some graphical artefacts (see here).

c <- ggplot(res, aes(x, y))
c +  stat_summary_hex(bins=40,aes(z = CONSO),fun = "sum", colour="grey") +
xlim(-9, 12) +
ylim(40, 52) +   
theme_void()

We then define a scale (both numeric and in terms of colors) using the scale_fill_viridis function. In order to better see large differences, we use the trans=”log” option which means that transitions between colors are logarithmic and not arithmetic progressions. The breaks points used are 1 GWh, 10 GWh, 100 GWh and 1 TWh.

 c <- ggplot(res, aes(x, y))
c +  stat_summary_hex(bins=40,aes(z = CONSO),fun = "sum", colour="grey") +
xlim(-9, 12) +
ylim(40, 52) +   
theme_void() +
scale_fill_viridis(
 option="A",
 trans = "log", 
 breaks = c(0,1000,10000,100000,1000000,99999999999),
 name="Electricity Consumption", 
 guide = guide_legend(keyheight = unit(2.5, units = "mm"),      keywidth=unit(4, units = "mm"), 
label.position = "bottom", 
title.position = 'top', nrow=1) )

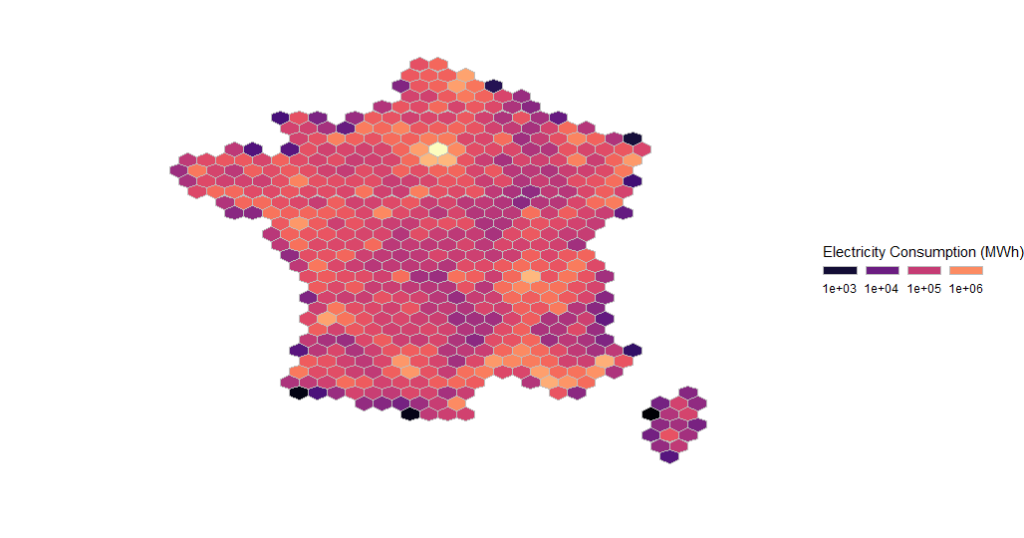
Using the following code with bins = 80 results in this another map:

c <- ggplot(res, aes(x, y))
c +  stat_summary_hex(bins=80,aes(z = CONSO),fun = "sum", colour="grey") +
xlim(-9, 12) +
ylim(40, 52) +   
theme_void() +
scale_fill_viridis(
 option="A",
 trans = "log", 
 breaks = c(0,1000,10000,100000,1000000,99999999999),
 name="Electricity Consumption", 
 guide = guide_legend(keyheight = unit(2.5, units = "mm"),      keywidth=unit(4, units = "mm"), 
label.position = "bottom", 
title.position = 'top', nrow=1) )

These map highlight the position of urban centers with high population density. A more useful information is the total electricity consumption per household (or, more accurately in this case, per energy delivery point, whose quantity per iris is PDL in the dataset), defined this way:

res$ElectricityPerHousehold <- res$CONSO/res$PDL

The code used to generate the map is slighty similar; the stat_summary_hex parameter are modified to aes(z = ElectricityPerHousehold) and fun=”mean”, and, scale_fill_viridis parameters are switched to option=”E” (leading to a new color scheme), new breakpoints of 2, 4, 6 and 8 GWh per household, and a new legend name.

 c <- ggplot(res, aes(x, y))
c +  stat_summary_hex(bins=80,aes(z = ElectricityPerHousehold),fun = "mean", colour="grey") +
xlim(-9, 12) +
ylim(40, 52) +   
theme_void() +
scale_fill_viridis(
 option="E",
 trans = "log", 
 breaks = c(0,2,4,6,8,10),
 name="Electricity Consumption per Household", 
 guide = guide_legend(keyheight = unit(2.5, units = "mm"),      keywidth=unit(4, units = "mm"), 
label.position = "bottom", 
title.position = 'top', nrow=1) )

This map better hightlights places with large electricity consumptions; Paris and its suburbs are associated to lower consumptions per household, which contrasts with an unusually high total consumption, due to high population density. An high consumption per household is usually associated to electric heating and/or large houses, and parisian dwellings are mostly smaller flats.

Featured image: Electricity Converter Power, by ArtisticOperations

Maquereaux et départements

Cette semaine, l’énigme “classique” de FiveThirtyEight (qu’on peut retrouver ici) demande de trouver des mots n’ayant aucune lettre en commun avec un et seul état américain. Par exemple, “mackerel” (le maquereau) a des lettres en commun avec tous les états sauf l’Ohio.

Ce problème peut s’adapter au cas français : quels sont les mots n’ayant aucune lettre en commun avec un et un seul département français ?

En reprenant la liste de mots utilisés pour notre article sur Motus et sur “Des Chiffres et des Lettres”, qui sont de 10 lettres au maximum (selon les règles des jeux), on trouve plus de 15 000 mots qui répondent à notre définition ! L’un d’entre eux est d’ailleurs “MAQUEREAUX”, qui partage (au moins) une lettre en commun avec tous les départements, sauf le Lot.

C’est d’ailleurs ce département qui est le plus souvent à l’origine de la présence des mots dans la liste ; c’est assez logique, car il ne contient ni A, ni E, ni I (lettres qui sont très présentes dans les autres départements), et ne contient que trois lettres.

En utilisant le dictionnaire Lexique, on peut chercher parmi des mots de plus de 10 lettres ceux qui répondent à notre définition. Le mot le plus long répondant à la définition est alors MULTIDIMENSIONNELLE, avec 19 lettres, grâce au département du Var.

Il est possible d’aller plus loin, si l’on accepte de compter tous les caractères des mots et non uniquement les lettres. Dans ce cas, avec 22 signes, le mot répondant à la définition est SUIVEZ-MOI-JEUNE-HOMME (oui, ce mot existe ; non, aucun lien avec les autres maquereaux) car il n’a aucune lettre en commun avec le Gard.

Comment trouver ces mots : description de l’algorithme

Le programme permettant de trouver les mots satisfaisant à la condition demandée (aucune lettre en commun avec un et un seul département) se décompose en plusieurs étapes.

Tout d’abord, on construit des matrices (des tableaux) dont chaque colonne est une lettre de l’alphabet et chaque ligne correspond à, soit un mot du dictionnaire, soit un département. Au croisement d’une ligne et d’une colonne se trouve une indicatrice TRUE/FALSE (qu’on recodera 1/0 après) indiquant si oui ou non la lettre se trouve dans le mot concerné. Pour cela, on utilise la fonction str_detect du package stringR.

sapply(LETTERS,FUN=str_detect,string="AIN")
A     B     C     D     E     F     G     H     I     J     K     L     M     N     O     P 
TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE TRUE FALSE FALSE 
Q     R     S     T     U     V     W     X     Y     Z 
FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

On a ainsi construit un tableau pour le dictionnaire tableau_dico et un tableau pour les départements tableau_dep. La commande suivante va calculer pour chaque mot du dictionnaire le nombre de département ne partageant aucune lettre en commun.

f <- function(x,ajout) {
  return(max(x + ajout))
}

sum(apply(tableau_dep,MARGIN = 1,f,ajout=tableau_dico[mot,]) == 1))

En décomposant un peu le code :

  • la fonction f construite ici prend deux vecteurs x et ajout et calcule le maximum de la somme des deux vecteurs ;
  • ici, ces deux vecteurs sont la ligne de tableau_dico associée au mot choisi et une ligne de tableau_dep, soit des vecteurs de 0 et 1 suivant si les lettres appartiennent aux mots considérés ;
  • f peut ici renvoyer 1 ou 2 : s’il renvoie 1, cela veut dire qu’il n’y a aucune lettre en commun, sinon, la valeur associée à cette lettre serait de 2, car somme de 1 et 1 dans chacun de deux vecteurs, et donc f calculerait un maximum de 2 ;
  • on applique cette fonction à l’ensemble des départements dans tableau_dep (apply avec le choix de margin=1 pour indiquer que l’on travaille sur les lignes) ;
  • on compte alors le nombre de départements pour lesquels cette sortie est 1.

Une fois qu’on a appliqué cette commande à l’ensemble des mots du dictionnaire, on peut enfin isoler les “maquereaux” en filtrant sur ceux pour lesquels le nombre de départements n’ayant aucune lettre en commun est exactement de 1.

Image : Atlantic mackerels (Petar Milošević)

Rolling some dices

Today, a quick post trying to provide an answer to this week Riddle Classic on FiveThirtyEight :

The fifth edition of Dungeons & Dragons introduced a system of “advantage and disadvantage.” When you roll a die “with advantage,” you roll the die twice and keep the higher result. Rolling “with disadvantage” is similar, except you keep the lower result instead. The rules further specify that when a player rolls with both advantage and disadvantage, they cancel out, and the player rolls a single die. Yawn!

There are two other, more mathematically interesting ways that advantage and disadvantage could be combined. First, you could have “advantage of disadvantage,” meaning you roll twice with disadvantage and then keep the higher result. Or, you could have “disadvantage of advantage,” meaning you roll twice with advantage and then keep the lower result. With a fair 20-sided die, which situation produces the highest expected roll: advantage of disadvantage, disadvantage of advantage or rolling a single die?

Extra Credit: Instead of maximizing your expected roll, suppose you need to roll N or better with your 20-sided die. For each value of N, is it better to use advantage of disadvantage, disadvantage of advantage or rolling a single die?

This problem is quite similar to some issues we’ve already tackled on this website, such as Tennis vs Badminton, or archery points (FR), or even how Eurovision rules impacts french rankings (FR). In order to answer we’re going to use simulations with R. The main set of functions needed is described here:

dice <- function() {return(sample(1:20,1))}

advantage <- function() {
  a <- dice()
  b <- dice()
  return(max(a,b))
} 

disadvantage <- function() {
  a <- dice()
  b <- dice()
  return(min(a,b))
} 

disadvantage_of_advantage <- function() {
   a <- advantage()
   b <- advantage()
   return(min(a,b))
 }

advantage_of_disadvantage <- function() {
   a <- disadvantage()
   b <- disadvantage()
   return(max(a,b))
 }

Then, we just need to simulate a fair amount (say, n = 10 000 or 100 000) of every dice rolling method. The first question to answer is: how to get the best rolls on average? The following graph answers it nicely, showing that the “disadvantage of advantage” method leads to better results than just rolling a dice, and even better ones than “advantage of disadvantage”.

Will this method be efficient for the other problem, which is maximising our chances to roll a value higher than a set threshold (resulting in harming the dragon, for instance, instead of failing miserably in our attempt)? The answer is yes… but only for lower values of the threshold!

As shown by the graph, as long as the threshold is 14 or higher (and killing a dragon might be that hard!), it’s better to just roll a dice. Why? That’s because our advantage and disadvantage modifiers tend to concentrate the distributions of values obtained: getting a 20 on “disadvantage of advantage” means that you need to get a 20 on both previous rollings with advantage, meaning that you need at least one 20 during each one ; this is extremly unlikely!

Eurovision 2020 – « prédictions »

L’Eurovision 2020, comme bon nombre d’événements culturels et sportifs, n’aura pas lieu cette année, pour cause de pandémie. Les chansons proposées par les pays participants ont néanmoins été mises en ligne : on peut les retrouver ici.

Même si cela n’a aucun intérêt (personne ne gagnera un concours qui n’aura pas lieu), il est donc possible de mettre en oeuvre notre modèle de prédictions (comme les années précédentes, en 2018 et 2019) utilisant les données associées à chaque vidéo sur Youtube : nombre de vues, “likes” – pouces vers le haut, “dislikes” – pouces vers le bas.

Le modèle utilise les données (Youtube et résultats lors du concours) pour les années précédentes et prédit ensuite le score qu’obtiendrait chaque pays. L’idée est que le nombre de personnes regardant un clip en ligne (et leurs réactions, via les boutons dédiés de Youtube) est un bon moyen de prédire le succès d’une chanson à l’Eurovision ; c’est évidemment très limité et ce pour de nombreuses raisons : existence d’un double vote (public et jury), différences entre les clips et la prestation en live, etc.

Passons donc aux « résultats » : our twelve points go to… la Russie !

En effet, comme en 2018 avec Israël, leur vidéo est un outlier (une observation avec des caractéristiques très différentes des autres) qui récolte plus de 85 millions de vues largement supérieur aux autres ; il s’agit de la chanson “Uno”, que vous pouvez (et je vous y encourage) écouter ci-après :

Sans surprise, ce sont donc eux qui sont les favoris pour notre modèle ! Le reste du top 5 (avec beaucoup moins d’écarts et donc de certitude) se compose de l’Arménie, l’Azerbaïdjan, l’Ukraine et la Bulgarie.

On peut comparer ces résultats (à défaut de ne jamais pouvoir savoir si le modèle aurait eu raison !) avec ceux des bookmakers (voir ici), évidemment gelés depuis l’annonce de l’annulation du concours. Ils ne plaçaient pas la Russie en premier, mais dans les cinq favoris néanmoins.

Comment expliquer la baisse de participation aux municipales 2020 ?

Dimanche dernier, le 15 mars 2020, la France a organisé le premier tour des élections municipales, après avoir annoncé une fermeture des écoles puis des restaurants et commerces non essentiels. La participation à ce scrutin s’établit à 44,64 %, en chute de 20 points par rapport à 2014, date des précédentes élections municipales (voir une très belle carte du Monde ici, assez illustrative de la situation)

Ce rapide billet ne s’attardera pas sur la question de savoir s’il fallait ou non organiser ces élections (le second tour est, lui, reporté à plus tard) ; nous cherchons ici à identifier quels sont les facteurs explicatifs de la baisse de participation aux municipales, et si ces facteurs peuvent avoir favorisé un ou plusieurs partis politiques.

Un sondage “jour de vote” réalisé par IFOP [modifié : je parlais dans la version initiale par erreur d’un sondage IPSOS ; celui-ci est consultable ici, et qui donne d’autres résultats encore, avec une plus forte participation à droite qu’à gauche sur l’échiquier politique] (consultable ici) montrait une importance du paramètre Covid-19 sur les raisons de ne pas aller voter (plus de 50% des sondés n’ayant pas voté jugeant que c’était une des raisons déterminantes), mais aussi une disparité entre les différentes familles politiques, avec une plus forte abstention chez les électeurs d’EELV (60 %) et une plus faible abstention chez les partisans d’En Marche (37 %).

Une analyse fine des résultats, bureau de vote par bureau, permet d’identifier les bureaux de vote pour lesquels l’évolution de l’abstention a été la plus forte entre 2014 et 2020 (on se limite au même scrutin des municipales), et, une fois ces bureaux de vote identifiés, analyser les résultats politiques obtenus au premier tour de l’élection présidentielle de 2017. Comme toujours, les données sont sur data.gouv.fr (ici pour les municipales 2020), merci à eux !

Le graphique ci-après résume les résultats obtenus :

On constate que les résultats ne sont pas les mêmes que ceux du sondage du jour du vote. Il semblerait que le vote Macron ou Le Pen, au premier tour en 2017, soit un bon indicateur d’une plus forte abstention aux municipales 2020. Cela ne veut cependant pas dire que les électeurs ayant choisi ces deux candidats sont plus sensibles au risques liées au Covid-19 ; peut-être est-ce plutôt lié à une séquence politique qui, pour les municipales 2020, n’était pas favorable à En Marche par exemple, même en l’absence de pandémie.

Méthodologie : les données relatives aux premiers tours des élections municipales de 2014 et 2020 ainsi que celles de la présidentielle 2017 sont agrégées au niveau du bureau de vote (on exclut ici les bureaux de vote ayant disparu, ayant fusionné ou ayant été créés). On calcule ensuite sur les un peu plus de 60 000 bureaux restants un différentiel de participation entre 2014 et 2020, qu’on régresse sur le taux parmi les votants pour chacun des candidats au premier tour de la présidentielle 2017.

Eurovision 2019 – prédictions

Sur le même modèle que l’année dernière (et, nous l’espérons, avec autant de succès !), nous allons tenter de faire nos prédictions pour l’Eurovision 2019, avec toujours un modèle basé sur les statistiques des vidéos publiées sur Youtube (la liste des vidéos en lice cette année est ici).

Les données

Rappel : nous utilisons les informations disponibles sur les vidéos Youtube : nombre de vues, nombre de “Like” et nombre de “Dislike”. Nous récupérons ces informations grâce au package R tuber, qui permet d’aller faire des requêtes par l’API de Youtube et ainsi de récupérer pour chacune des vidéos d’une playlist les informations nécessaires pour le modèle. Ces informations sont ensuite complétées (pour les années 2016, 2017 et 2018) avec le nombre de points obtenus et le rang du classement final.

Par rapport à l’année dernière, on dispose donc d’une année supplémentaire pour l’apprentissage du modèle (pour rappel, les modalités de calcul des points ont changé en 2016, donc on ne peut pas facilement utiliser des éditions antérieures).

Le modèle

L’objectif principal est d’estimer le score que chaque pays va avoir, afin de pouvoir construire le classement final. La méthode utilisée est toujours la régression linéaire sur les variables disponibles (nombre de vues, nombre de “Likes”, nombre de “Dislikes”)

Pour le modèle utilisant uniquement les données 2016 et 2017, calculé l’année dernière, on rappelle que le nombre de vues ne joue pas significativement, le nombre de Likes de façon très mineure et le nombre de Dislikes très nettement, avec un lien positif : plus il y a de pouces baissés, plus le score est important. Ce résultat atypique peut s’expliquer par le fait que la vidéo ukrainienne en 2016, gagnante, a plus de 40 000 pouces baissés.

(Mise à jour : une première version de ce post contenait des erreurs sur le second modèle) Le modèle intégrant les données 2018 (prises quelques semaines avant la finale) en plus change légèrement. Il accorde moins de valeur au nombre de Dislikes (cela peut s’expliquer par le fait que la chanson russe en 2018 avait un nombre de pouces baissés très important, mais n’a pas accédé à la finale, donc n’a pas obtenu un résultat très bon), mais associe désormais positivement le nombre de vues et le score (ce qui n’était pas le cas avant, étonnement).

Ce modèle, construit à partir de plus de données, est celui privilégié ; on comparera tout de même les résultats obtenus par les deux modèles à la fin de cet article !

Les résultats

Voici les prédictions obtenues, en utilisant le modèle comprenant les données de 2016 à 2018 et appliqué aux données Youtube 2019 :

Le grand gagnant serait Malte. Ils ne sont pas dans les favoris des bookmakers : voir ici, par exemple, ou plus largement avec les données des paris ici : à la date d’extraction des données, le 30 avril, Malte était classée 8ème.

Voici la vidéo proposée par Malte pour l’Eurovision 2019 (dont l’artiste Michela Pace illustre cette publication) :

Les Pays-Bas sont seconds dans notre modèle. Ce sont eux les grands favoris pour l’instant, avec “Arcade” :

Et pour la France ? 10ème selon notre modèle, 11ème selon les bookmakers, nous ne serons pas a priori les Rois de la compétition :

Mais, quand on sait que la vidéo de Bilal sur sa chaîne Youtube personnelle enregistre presque 6 millions de vues, peut-on penser qu’il y a un biais à ce niveau-là ? À suivre…

Mise à jour au 7 mai : le modèle avec les nouvelles données Youtube donne des résultats identiques :

Et avec l’autre modèle ?

En utilisant le modèle comprenant les données de 2016 et 2017 uniquement (et donc, sans 2018), on obtient les résultats suivants, avec, en bleu, les pays pour lesquels le score prédit aurait été plus fort, et en rouge ceux pour qui il aurait été plus faible :

Ce modèle conduit à favoriser les Pays-Bas, et renvoie Malte bien plus bas dans le classement ; mais il se base fortement sur les Dislikes, ce qui n’avait pas été pertinent en 2018… À suivre également !

Ranking places with Google to create maps

Today we’re going to use the googleway R package, which allows their user to do requests to the GoogleMaps Places API. The goal is to create maps of specific places (restaurants, museums, etc.) with information from Google Maps rankings (number of stars given by other people). I already discussed this in french here to rank swimming pools in Paris. Let’s start by loading the three libraries I’m going to use : googleway, leaflet to create animated maps, and RColorBrewer for color ranges.

library(googleway)
library(leaflet)
library(RColorBrewer)

First things first. To do API request to Google, we need an API key ; you can ask for one here. We’ll use this key for the rest of the program, so let’s declare a global variable :

api_key <- "YourKeyHereIWontGiveYouMine"

Retrieving Google Data

We’re going to use the google_places function to get a list of places matching a description, called research in my program (for instance : “Restaurant, Paris, France”). The output are multiple, and I’m going to store the place ID and the rating. I’ll also store the research token ; that’ll be explained later.

gmaps_request <- google_places(search_string = research, language = language, key = api_key)
  gmaps_data <- gmaps_request$results
  
  place_id <- gmaps_data$place_id
  rating <- gmaps_data$rating
  
  token <- gmaps_request$next_page_token

This function returns up to 20 places associated to the research by Google. If you want more than 20, you need to use the token previously stored in order to ask the Google Places API to give you the next results, by tweaking the function this way :

gmaps_request <- google_places(search_string = research, language = language, key = api_key, page_token = token)

There are tow caveats to this function. Firstly, the token can be NULL. In this case, there isn’t any further research results you can get. This happens automatically as soon as you reach 60 results. Secondly, the API needs time to refresh the token research (see here) ; that’s why we’re going to make R wait a few seconds, using Sys.sleep(time) between our requests. Our complete function is therefore :

gmaps_request <- google_places(search_string = research, language = language, key = api_key)
  gmaps_data <- gmaps_request$results
  
  place_id <- gmaps_data$place_id
  rating <- gmaps_data$rating
  
token <- gmaps_request$next_page_token
Sys.sleep(5)
continue <- TRUE

  while (continue) {
    
    gmaps_request <- google_places(search_string = research, language = language, key = api_key, page_token = token)
    gmaps_data <- gmaps_request$results
    
    if (!is.null(gmaps_request$next_page_token)) {
      place_id = c(place_id,gmaps_data$place_id)
      rating = c(rating,gmaps_data$rating)
      token <- gmaps_request$next_page_token
      Sys.sleep(5)
    }
    else{continue <- FALSE}
  }

Now we’re going to search for the spatial coordinates of the places we found. To this extent, we’re going to use the google_place_details function of the packages, and retrieve latitude and longitude with these two functions :

get_lat <- function(id, key, language) {
  id <- as.character(id)
  details <- google_place_details(id, language = language, key=key)
  return(details$result$geometry$location$lat)
}

get_lng <- function(id, key, language) { 
  id <- as.character(id)
  details <- google_place_details(id, language = language, key=key)
  return(details$result$geometry$location$lng) 
}

All these blocks add up to build the complete function :

get_gmaps_data <- function(research, api_key, language) {
  
  gmaps_request <- google_places(search_string = research, language = language, key = api_key)
  gmaps_data <- gmaps_request$results
  
  place_id <- gmaps_data$place_id
  rating <- gmaps_data$rating
  
  token <- gmaps_request$next_page_token
  Sys.sleep(5)
  continue <- TRUE
  
  while (continue) {
    
    gmaps_request <- google_places(search_string = research, language = language, key = api_key, page_token = token)
    gmaps_data <- gmaps_request$results
    
    if (!is.null(gmaps_request$next_page_token)) {
      place_id <- c(place_id, gmaps_data$place_id)
      rating <- c(rating, gmaps_data$rating)
      token <- gmaps_request$next_page_token
      Sys.sleep(5)
    }
    else{continue <- FALSE}
  }
  
  lat = sapply(place_id, get_lat, key=api_key, language=language)
  lng = sapply(place_id, get_lng, key=api_key, language=language)
  
  return(data.frame(place_id, rating, lat, lng))
}

Map plot

The next part is more classical. We’re going to order the ratings of the data frame built by the previous function in order to arrange the places in differents groups. Each of the groups will be associated to a color on the data plot. If we want to make number_colors groups with the color scheme color (for instance, “Greens”), we are using the following instructions :

color_pal <- brewer.pal(number_colors, color)
pal <- colorFactor(color_pal, domain = seq(1,number_colors))

plot_data <- gmaps_data
plot_data$ranking <- ceiling(order(gmaps_data$rating)*number_colors/nrow(plot_data))

The definitive function just needs the addition of the leaflet call :

show_map <- function(number_colors, gmaps_data, color="Greens") {
  
color_pal <- brewer.pal(number_colors,color)
pal <- colorFactor(color_pal, domain = seq(1,number_colors))

plot_data <- gmaps_data
plot_data$ranking <- ceiling(order(gmaps_data$rating)*number_colors/nrow(plot_data)) leaflet(plot_data) %>% addTiles() %>%
  addCircleMarkers(
    radius = 6,
    fillColor = ~pal(ranking),
    stroke = FALSE, fillOpacity = 1
  ) %>% addProviderTiles(providers$CartoDB.Positron)
}

Examples

I just need to combine these two functions in one, and then to do some food-related examples !

maps_ranking_from_gmaps <- function(research, api_key, language, number_colors=5, color="Greens") {
  show_map(number_colors, get_gmaps_data(research, api_key, language), color)
}

maps_ranking_from_gmaps("Macaron, Paris, France", api_key, "fr")
maps_ranking_from_gmaps("Macaron, Montreal, Canada", api_key, "fr")

maps_ranking_from_gmaps("Poutine, Montreal, Canada", api_key, "fr", 5, "Blues")
maps_ranking_from_gmaps("Poutine, Paris, France", api_key, "fr", 5, "Blues")

which returns the following maps :

Macaron in Paris, France

Macaron in Montreal, Canada

Poutine in Montreal, Canada

Poutine in Paris, France (I guess French people are not ready for this)

Est-ce que cette piscine est bien notée ?

J’ai pris la (mauvaise ?) habitude d’utiliser Google Maps et son système de notation (chaque utilisateur peut accorder une note de une à cinq étoiles) pour décider d’où je me rend : restaurants, lieux touristiques, etc. Récemment, j’ai déménagé et je me suis intéressé aux piscines environnantes, pour me rendre compte que leur note tournait autour de 3 étoiles. Je me suis alors fait la réflexion que je ne savais pas, si, pour une piscine, il s’agissait d’une bonne ou d’une mauvaise note ! Pour les restaurants et bars, il existe des filtres permettant de se limiter dans sa recherche aux établissements ayant au moins 4 étoiles ; est-ce que cela veut dire que cette piscine est très loin d’être un lieu de qualité ? Pourtant, dès lors qu’on s’intéresse à d’autres types de services comme les services publics, ou les hôpitaux, on se rend compte qu’il peut y avoir de nombreux avis négatifs, et des notes très basses, par exemple :

Pour répondre à cette question, il faudrait connaître les notes qu’ont les autres piscines pour savoir si 3 étoiles est un bon score ou non. Il serait possible de le faire manuellement, mais ce serait laborieux ! Pour éviter cela, nous allons utiliser l’API de GoogleMaps (Places, vu qu’on va s’intéresser à des lieux et non des trajets ou des cartes personnalisées).

API, késako? Une API est un système intégré à un site web permettant d’y accéder avec des requêtes spécifiques. J’avais déjà utilisé une telle API pour accéder aux données sur le nombre de vues, de like, etc. sur Youtube ; il existe aussi des API pour Twitter, pour Wikipedia…

Pour utiliser une telle API, il faut souvent s’identifier ; ici, il faut disposer d’une clef API spécifique pour Google Maps qu’on peut demander ici. On peut ensuite utiliser l’API de plusieurs façons : par exemple, faire une recherche de lieux avec une chaîne de caractères, comme ici “Piscine in Paris, France” (avec cette fonction) ; ensuite, une fois que l’on dispose de l’identifiant du lieu, on peut chercher plus de détails, comme sa note, avec cette fonction. De façon pratique, j’ai utilisé le package googleway qui possède deux fonctions qui font ce que je décris juste avant : google_place et google_place_details.

En utilisant ces fonctions, j’ai réussi à récupérer de l’information sur une soixantaine de piscines à Paris et ses environs très proches (je ne sais pas s’il s’agit d’une limite de l’API, mais le nombre ne semblait pas aberrant !). J’ai récupéré les notes et je constate ainsi que la note moyenne est autour de 3.5, ce qui laisse à penser que les piscines à proximité de mon nouvel appartement ne sont pas vraiment les meilleures… De façon plus visuelle, je peux ensuite représenter leur note moyenne (en rouge quand on est en dessous de 2, en vert de plus en plus foncé au fur et à mesure qu’on se rapproche de 5) sur la carte suivante (faite avec Leaflet, en utilisant le très bon package leaflet)

Comparaison avec d’autres lieux

En explorant Google Maps aux alentours, je me suis rendu compte que les agences bancaires du quartier étaient particulièrement mal notées, en particulier pour une banque spécifique (dont je ne citerai pas le nom – mais dont le logo est un petit animal roux). Je peux utiliser la même méthode pour récupérer par l’API des informations sur ces agences (et je constate qu’effectivement, la moyenne des notes est de 2 étoiles), puis les rajouter sur la même carte (les piscines correspondent toujours aux petits cercles ; les agences bancaires sont représentées par des cercles plus grands), en utilisant le même jeu de couleurs que précédemment :

La carte est difficile à lire : on remarque surtout que les petits cercles (les piscines) sont verts et que les grands (les agences bancaires) sont rouges. Or, il pourrait être intéressant de pouvoir comparer entre eux les lieux de même type. Pour cela, nous allons séparer au sein des piscines les 20% les moins bien notées, puis les 20% d’après, etc., et faire de même avec les agences bancaires. On applique ensuite un schéma de couleur qui associe du rouge aux 40% des lieux les pires – relativement (40% des piscines et 40% des agences bancaires), et du vert pour les autres. La carte obtenue est la suivante : elle permet de repérer les endroits de Paris où se trouvent, relativement, les meilleurs piscines et les meilleures agences bancaires en un seul coup d’œil !

Google introduit des modifications aux notes (en particulier quand il y a peu de notes, voir ici (en), mais pas seulement (en)) ; il pourrait être intéressant d’ajouter une fonctionnalité permettant de comparer les notes des différents lieux relativement aux autres de même catégorie !

[Sampling] Présentation à Ottawa – une nouvelle base pour les enquêtes de l’INSEE

Demain (jeudi 8 novembre), je donnerai une présentation au Symposium de méthodologie de Statistiques Canada sur la mise en place du nouveau système d’échantillonnage de l’INSEE pour les enquêtes auprès des ménages et des individus à partir des sources fiscales.

Ce changement de base apporte de nouvelles opportunités (nouvelles variables, nouveaux moyens de contact, meilleure coordination des enquêtes) mais aussi des défis (concordance des concepts, gestion du champ de la base administrative).

Les acétates sont ci-dessous :

Analyse de pronostics pour le Mondial 2018

On est les champions ! Si nous n’avons pas eu le temps de faire un modèle de prédiction pour cette coupe du monde de football 2018 (mais FiveThirtyEight en a fait un très sympa, voir ici), cela ne nous a pas empêché de faire un concours de pronostics entre collègues et ex-collègues statisticiens, sur le site Scorecast. Les résultats obtenus sont les suivants :

JoueurScore
Nic102
Cle100
Ron100
Lud96
Tho90
Lio88
Lis87
Pap86
Mau84
Yan78
Ant78
Lau75
Thi71
Arn56
Oli28
Mar7

Un autre système de points ?

Le système de points utilisé par Scorecast est le suivant : si on a le bon gagnant, on gagne un faible nombre de points ; si en plus du bon gagnant, on a bien prédit l’écart de buts, on gagne un peu plus de points ; et enfin, si on a le score exact, on gagne le nombre maximal de points. Ce nombre maximal de points augmente au fur et à mesure de la compétition : la finale vaut plus de points qu’un match de poules. Ce système ne tient pas compte de cotes préexistantes (comme le fait par exemple Mon petit prono), ou du fait que certains matchs sont bien prédits par tout le monde alors que pour d’autres seule une personne a bien trouvé, voire personne.

Je propose donc ici d’altérer légèrement l’attribution des points, de la façon suivante : on dispose d’un nombre de points équivalent pour chaque match d’une même manche (match de poule, de quart, etc.), qu’on répartit entre les joueurs qui ont bien prédit le score, avec un avantage pour ceux qui ont le bon écart de points ou le bon score exact. Le nombre de points à répartir augmente tout au long de la compétition, de sorte que les phases finales aient plus d’importance dans le classement final.

Pourquoi faire ça ? Pour favoriser les joueurs qui ont fait des paris plus originaux et potentiellement plus risqués, ou en tout cas qui étaient les seuls à avoir la bonne intuition. Voici les résultats :

JoueurScoreScore modifié
Mau84185
Lud96163
Nic102144
Tho90136
Ant78135
Cle100126
Ron100123
Lis87120
Lio88115
Pap86108
Yan78105
Lau75100
Thi7190
Arn5678
Oli2843
Mar710

On constate que le classement évolue sensiblement avec cette nouvelle méthode de points ! Mais peut-être que certains auraient fait d’autres paris si ces règles étaient décidées…

Choix des scores

Une des principales difficultés du pronostic est qu’il ne suffit pas de savoir (ou de penser savoir) qui va gagner le match, mais il faut aussi indiquer le score attendu. Regardons si les prédictions de l’ensemble des parieurs de notre ligue ont été pertinentes par rapport aux vrais scores ! Pour cela, on détermine pour chaque score le pourcentage des matchs qui ont abouti à ce résultat d’une part, et le pourcentage des paris faits avec ce score. On regarde ensuite la différence entre les pourcentages, qu’on va illustrer par la heatmap ci-dessous. Les cases vertes correspondent aux scores des matchs trop rarement prédits ; les cases rouges aux scores très souvent prédits mais qui n’arrivent que peu ou pas.

On constate que l’on a surestimé largement le nombre de 2-1, de 3-0 et de 4-0 (score qui n’est jamais arrivé lors de cette coupe du monde) ; ce sont d’ailleurs les seuls “gros” scores qui ont été surestimés dans les prédictions : tous les autres ont été sous-évalués. Cela peut laisser penser que les paris ont été faits avec une logique conservative et en évitant de tenter des scores absurdes, comme 7-0 pour l’Arabie Saoudite contre la Russie !

Analyse de données et classification

Enfin, une dernière utilisation possible de ce jeu de données est d’en faire l’analyse pour en extraire des classes de parieurs ayant un peu le même profil (ou en tout cas les mêmes réussites), et pour voir ce qui les sépare. Plusieurs méthodes sont possibles pour cela.

Commençons par un grand classique : la Classification Ascendante Hiérarchique (CAH pour les intimes), qui est une méthode qui part de groupes d’une personne, et qui, à chaque étape, regroupe deux groupes de telle façon à ce que l’inertie intra augmente au minimum. De façon moins barbare, cela veut dire qu’on regroupe les deux groupes qui se ressemblent le plus, étape par étape, jusqu’à arriver à la population totale. On représente souvent ce type de méthodes par un dendogramme, qui ressemble un peu à un arbre phylogénétique en biologie de l’évolution, et qui illustre la construction des classes, de bas en haut.

On remarque qu’il y a de nombreux binômes qui sont cohérents, et qui signalent des parieurs avec des profils comparables (par exemple, Mar et Oli, qui correspondent à deux joueurs ayant raté une bonne partie de la compétition, soit en arrêtant les paris, soit en arrivant en cours), et qu’il y a une séparation entre les quatre joueurs de gauche et les autres (eux-mêmes largement séparés entre les 3 les plus à gauche et les autres).

Une autre possibilité est d’utiliser l’Analyse en Composantes Principales, que nous avions déjà utilisé dans un contexte footballistique ici ou ici (en). La logique est ici de chercher à résumer une matrice avec beaucoup d’informations (pour chaque joueur, l’ensemble des points obtenus via ses paris pour chaque match) en un nombre minimal de dimensions, dits d’axes, qui suffisent pour avoir une bonne idée de la logique d’organisation du jeu de données.

Si l’on réalise cette méthode ici, voici ce que l’on obtient sur les premiers axes :

L’axe 1 est souvent victime de ce qu’on appelle l'”effet taille” : on entend par là le fait que les individus ayant de grandes valeurs de certaines variables en ont souvent aussi pour les autres variables, et symétriquement pour les individus qui ont des petites valeurs. En effet, on voit que la variable supplémentaire, le total de points obtenus (avec la méthode Scorecast), en bleu, est proche de l’axe 1. Cela veut dire que les individus à droite de l’axe ont tendance à avoir un score important, tandis que ceux à gauche n’ont pas très bien réussi leurs prédictions.

On constate également que les représentations sur les plans constitués des dimensions 1-2, et 2-3, ont tendance à rapprocher les individus que la classification effectuée plus haut associait en binôme. Cela montre une certaine cohérence, ce qui est toujours rassurant !

Plus dans le détail, on voit que les axes 2 et 3 semblent correspondre aux paris suivants, qui sont donc discriminants entre les différents joueurs :

  • Pour l’axe 2, avoir réussi son pari sur les matchs Pérou-Danemark, Mexique-Suède, Brésil-Suisse, Espagne-Russie et Argentine-Croatie
  • Pour l’axe 3, avoir réussi son pari sur les matchs Japon-Sénégal, Suisse-Costa Rica, Danemark-France ou encore Brésil-Mexique

Difficile de trouver une interprétation de ces axes…